Professional Documents
Culture Documents
Terminado Teoria de Campos
Uploaded by
Jhan Carlos Bran ReyesCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Terminado Teoria de Campos
Uploaded by
Jhan Carlos Bran ReyesCopyright:
Available Formats
FACULTAD DE CIENCIAS NATURALES Y MATEMATICA ESCUELA DE PROFESIONAL DE FISICA TEMA: TENSOR DE RIEMANN
ALUMNO: BRAN REYES JHAN CARLOS
CURSO: TEORIA CLASICA DE CAMPOS
PROFESOR: ESPICHAN
CICLO: 2012
Introducion Riemann cre el tensor mtrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les haca posible expresar a partir del famoso teorema de Pitgoras. (Claro que, es una herramienta para utilizar en un mundo tridimensional). El tensor mtrico de Riemann, o N dimensiones, fue mucho ms all y podemos decir que es el teorema para dimensiones ms altas con el que podemos describir fenmenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmsfera, como por ejemplo tambin la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann, permiti a Einstein formular su teora de la gravedad y, posteriormente lo utilizo Kaluza y Klein para su teora en la quinta dimensin de la que aos ms tarde se derivaron las teoras de supergravedad, supersimetra y, finalmente las supercuerdas.
El tensor de Riemann En la Teora General de la Relatividad, hay tres tensores que nos interesan para estudiar y especificar la curvatura de un espacio-tiempo curvo: el tensor de Einstein G, el tensor de Ricci y el tensor de Riemann R. El tensor de Einstein es obtenido a partir del tensor de Ricci, y a su vez el tensor de Ricci es obtenido a partir del tensor de Riemann, el tensor de Riemann esta relacionado con la curvatura en un espacio multi-dimensional deriva de dicho tensor. El tensor de Riemann surge como consecuencia del anlisis involucrado en dar respuesta a lo que parece ser una pregunta sencilla. Empezando con un tensor covariante V = (Vi) y tomando la derivada covariante del tensor primero con respecto a la coordenada x j y luego con respecto a la coordenada xk nos produce un tensor de tercer orden: ((Vi); j); k = (Vi); jk = Vi; jk Pero que tal si tomamos primero tomando la derivada covariante del tensor primero con respecto a la coordenada xk y luego con respecto a la coordenada x j?: ((Vi); k); j = (Vi); kj = Vi; kj Es importante el orden en el cual se lleve a cabo la diferenciacin, o se puede decir que en general Vi; jk = Vi; kj? En la diferenciacin parcial ordinaria, no parece haber duda alguna al respecto, ya que las diferenciaciones mltiples se pueden llevar a cabo en el orden que sea:
Pero al estar trabajando con tensores, se tiene que llevar a cabo usando la derivada covariante.
PROBLEMA: Demostrar que Vp;qr - Vp;rq no es igual a cero, y que por lo tanto el orden de la diferenciacin covariante s afecta el resultado final. En el primer paso, evaluaremos primero la derivada covariante mltiple Vp;qr aplicando la definicin de la derivada covariante para un tensor covariante:
Aplicando la definicin de la derivada covariante para un tensor covariante: se tiene
Efectuando los parntesis
Hemos obtenido ya Vp;qr. Repitiendo el procedimiento, podemos obtener tambin Vp;rq, pero no es necesario hacerlo todo de nuevo, ya que basta con intercambiar el orden de los ndices para obtener Vp;rq. Hecho esto, si restamos Vp;rq de Vp;qr obtenemos entonces:
Podemos renombrar los ndices para poner en los cuatro trminos al tensor Vj como producto:
Esto nos permite llevar a cabo la siguiente factorizacin:
A menos de que los smbolos de Christoffel sean todos iguales a cero, lo cual no ocurre en un espacio multi-dimensional plano, Vp;qr y Vp;rq no son iguales, son diferentes, y son diferentes precisamente en una cantidad como la mostrada en color azul entre los parntesis. Dicha cantidad:
simbolizada tensorialmente como Rjpqr es precisamente lo que se conoce como el tensor de Riemann. El que Vp;qr Vp;rq El tensor de curvatura de Riemann, o simplemente tensor de Riemann, es un tensor de orden cuatro, de modo tal que los componentes de dicho tensor no pueden ser visualizados con una representacin matricial como ocurre con el caso de un tensor mtrico g de orden 2. En el caso Rabcd (todos los cuatro ndices abajo) llamamos al tensor un tensor de Riemann del primer gnero primera especie (first kind) mientras que en el caso Ra bcd (el primer ndice elevado) llamamos al tensor un tensor de Riemann del segundo gnero segunda especie (second kind). Formalmente, y en base al resultado obtenido al principio, el tensor de Riemann del segundo gnero se puede definir a partir de los smbolos de Christoffel (los cuales no son tensores) de la siguiente manera (obsrvese con detenimiento el uso de la derivada parcial ordinaria, indicado por la coma puesta antes del ndice utilizado para la diferenciacin!): Ra bcd = abd,c - abc,d + ac bd - ad bc Puesto de manera ms explcita:
Ra bcd =__________________________ (abd)/xc - (abc)/xd + abc,d + ac bd - ad bc Si utilizamos el tensor de Riemann para el estudio de un espacio de cuatro dimensiones como ocurre en el caso del espacio-tiempo de la Teora General de la Relatividad, cada uno de los cuatro sub-ndices del tensor de Riemann puede representar una de cuatro variables diferentes, as que un tensor de Riemann est especificado por un total de 4x4x4x4 = 256 componentes, lo cual nos puede parecer intimidante. Sin embargo, debido a las simetras que presenta este tensor, no todas las componentes son independientes, lo cual reduce el nmero de componentes que tienen que ser calculadas de 256 a 36. Una de tales simetras en el intercambio del tercer y cuarto ndice es la siguiente: Ra bcd = - Ra bdc Imponiendo adems la condicin adicional: Ra bcd + Ra cdb + Ra dbc = 0 el nmero de componentes independientes puede ser reducido posteriormente a 21, y si se satisface una identidad adicional el nmero de componentes puede ser reducido a 20. Poniendo las componentes del tensor de Riemann R = (R) del primer gnero en funcin de las componentes de un tensor mtrico g, podemos obtener la siguiente expresin (de nueva cuenta, las comas en los sub-ndices indican derivadas parciales ordinarias): R = (g, - g, + g, - g,)/2
PROBLEMA: A partir de la definicin del tensor de Riemann de primer gnero, demostrar las identidades: R = - R
R = - R R = R R + R + +R = 0 1) A partir de la definicin de los componentes R en funcin de los componentes derivados del tensor mtrico: R = (g, - g, + g, - g,)/2 intercambiamos los ndices y obteniendo lo siguiente: R = (g, - g, + g, - g,)/2 y tras un simple reacomodo: R = (-g, + g, - g, + g,)/2 R = - R 2) Procediendo como lo hicimos arriba, intercambiando los ltimos dos ndices y : R= (g, - g, + g, - g,)/2 y reacomodando: R = (-g, + g, - g, + g,)/2 R = - R 3) Intercambiando el primer par de ndices con respecto al segundo par de ndices (lo cual debe ser interpretado como dos operaciones, la primera siendo el intercambio de los ndices y , y la segunda siendo el intercambio de los ndices y ): R = (g, - g, + g, - g,)/2
Podemos efectuar un ligero reacomodo de ndices, haciendo adems uso del hecho de que las derivadas parciales ordinarias se pueden llevar a cabo en cualquier orden, esto es: g, = g, obteniendo as lo siguiente: R = ( g, - g, + g, - g,)/2 Por otro lado, puesto que el tensor mtrico es simtrico, tenemos que: g = g con lo cual lo anterior se nos reduce a: R = (g, - g, + g, - g,)/2 y con otro ligero reacomodo: R = ( g, - g, + g, - g,)/2 R = R 4) Finalmente, escribiendo la suma de los tres trminos involucrados en la primera identidad de Bianchi tras obtener los otros dos trminos mediante un intercambio de ndices, y simplificando con la ayuda de la simetra de los componentes del tensor mtrico: R + R + R = (g, - g, + g, - g,)/2 (g, - g, + g, - g,)/2 (g, - g, + g, - g,)/2 obtenemos el resultado final deseado, la primera identidad de Bianchi:
R + R + R = 0 PROBLEMA: Cuntos componentes independientes de R puede haber para un espacio de tres dimensiones? Cules son estos componentes? Para un espacio de tres dimensiones, el nmero de componentes posibles es, de acuerdo a la frmula general: n (n - 1) /12 = 3 (3 -1) /12 = (9)(8)/12 = 6 Estos componentes son los siguientes: R1212 , R1313 , R2323 , R1213 , R2123 , R3132 Hay otra manera de llegar al tensor de Riemann, y esta es mediante el uso del concepto del transporte paralelo, porque el tensor de Riemann es de hecho una descripcin matemtica de la curvatura intrnseca de una hoja. Para ello, recurrimos al transporte paralelo de un vector V alrededor de una trayectoria cerrada que nos regrese al punto de origen despus de darle una vuelta completa a un pedazo de superficie. Identificaremos a este pedacito de superficie como un parche de coordenadas (coordinate patch) cortado con unas tijeras imaginarias de la hoja (manifold) mostrada en la figura de abajo. De este modo, imaginemos en nuestra hoja un pedacito muy pequeo de superficie cuyos cuatro lados coinciden con las lneas de coordenadas x1 = a, x1 = a + a, x2 = b y x2 = b + b:
Trasladamos mediante transporte paralelo al vector V .Empezando desde el punto A hasta el punto A completando de este modo un circuito cerrado. La trayectoria completa del vector V a lo largo de la retcula de coordenadas (x1, x2) es: Ruta 1: A(a, b) B(a + a, b) Ruta 2: B(a + a, b) C(a + a, b + b) Ruta 3: C(a + a, b + b) D(a, b + b) Ruta 4: D(a, b + b) A(a, b) Tomaremos ahora una enunciacin simblica usual de la operacin de transporte paralelo (en la cual el smbolo no representa al operador vectorial diferencial usual) que representa al transporte paralelo del vector V a lo largo de la trayectoria U:
y haremos U = e1 simbolizando con esto el transporte paralelo del vector V a lo largo del vector tangente a la coordenada x1:
Para fines de clculo, tensorialmente hablando, esta simbolizacin en realidad no es ms que la derivada absoluta o derivada intrnseca que involucra dos operaciones distintas: (1) la obtencin de la derivada covariante de V y (2) la contraccin tensorial con el vector U:
Expandiendo la sumatoria mltiple en la operacin de transporte paralelo que estamos considerando, llevada a cabo a lo largo de e1, tenemos entonces:
U1V;1 = 0
Aqu podemos aplicar directamente la definicin de la derivada covariante a V (usaremos la notacin de la coma para denotar la diferenciacin parcial con respecto a la coordenada x1: U1(V,1 + 1V) = 0 Puesto que la trayectoria (y consecuentemente la tangente a la trayectoria) a lo largo de la coordenada x1 no es nula, entonces el factor entre los parntesis debe de serlo: V,1 + 1V = 0 V,1 = - 1V o bien, explcitamente:
Con esto, si llevamos a cabo una integracin de cada una de las componentes de V = (V) desde el punto A hasta el punto B:
tenemos entonces lo siguiente con el resultado que hemos obtenido:
Procediendo del mismo modo, obtenemos lo siguiente para la ruta que lleva mediante transporte paralelo al vector V desde el punto B hasta el punto C:
Para la ruta que lleva mediante transporte paralelo al vector V desde el punto C hasta el punto D tenemos lo siguiente:
Y por ltimo, la ruta que lleva mediante transporte paralelo al vector V desde el punto Dhasta el punto A est dada por la siguiente relacin:
Obsrvese que, V(A) que parte del punto A y el vector V(A) que llega al punto A despus de un recorrido completo se han simbolizado de color distinto, uno azul y el otro rojo. Esto se debe a que despus de recorrer el circuito completo el vector V apuntar a una direccin diferente en relacin a la direccin a la cual apuntaba al iniciar el recorrido en virtud de haberse hecho el recorrido sobre una superficie curva(como la superficie de una esfera). La nica forma posible en la cual el vector V puede ser exactamente el mismo despus del recorrido A-B-C-D mediante el transporte paralelo es que el parche de coordenadas corresponda a una superficie plana. Si llamamos al cambio neto en el vector V = (V) como V, definido de la siguiente manera: V = V(A) - V(A) entonces este cambio neto se puede obtener sumando todas las integrales obtenidas arriba:
Adems de haberse sumado los trminos, se ha llevado a cabo una inversin en los lmites de las integrales de la ruta 3 (de C a D) y de la ruta 4 (de D a A), lo cual tiene como efecto matemtico la inversin de signos, y se han reacomodado las integrales para que el siguiente paso sea ms obvio. A primera vista, se antoja de inmediato una cancelacin de los trminos. La integral de laruta 1 (de A a B) puesta en color azul y con signo negativo parece que puede ser cancelada por la integral de la ruta 3 (de C a D) puesta en color rojo, de signo positivo. Lo mismo puede decirse para el otro par de integrales. Sin embargo, para que pueda efectuarse dicha cancelacin, se requiere para el primer par que tanto 1 como V sean trminos constantes, y no lo son. Seran constantes en un espacio-tiempo plano. Pero ciertamente no son constantes en un espacio-tiempo curvo. Puesto de otra manera:
Y lo mismo puede decirse para el otro par de integrales. Ante esta situacin, podemos recurrir a una aproximacin de primer orden mediante una serie de Taylor-McLaurin, la cual para una funcin F de dos variables x1 y x2 es la siguiente cuando es desarrollada en torno a un punto P(x1,x2) = P(m,n):
Descartando los trminos de orden superior, de esta expansin en serie de TaylorMacLaurin obtenemos la siguiente expresin cuando la coordenada x1 se mantiene constante (esto ocurre al llevar a cabo el transporte paralelo del vector V del punto A al punto B, y del punto C al punto D):
Y de la misma manera obtenemos la siguiente expresin cuando la coordenada x2 se mantiene constante (esto ocurre al llevar a cabo el transporte paralelo del vector V del punto B al punto C, y del punto D al punto A):
De este modo, podemos obtener la siguiente aproximacin a un primer orden a la variacin neta del vector V al llevarse a cabo la operacin de transporte paralelo :
Podemos sacar fuera de cada una de estas integrales lo que no es afectado por el proceso de integracin de acuerdo con la variable que est siendo integrada:
Las dos integrales son triviales, y llevndolas a cabo tenemos lo siguiente:
Factorizando y reagrupando:
El siguiente paso consiste en tomar las diferenciales aplicando la regla de Leibniz para la diferencial del producto de dos funciones:
Podemos simplificar esto eliminando las derivadas de V utilizando para ello el resultado derivado al principio usando adems su equivalente reemplazando el ndice 1 con un ndice 2:
De este modo, obtenemos lo siguiente, usando la notacin de la coma para indicar diferenciacin ordinaria: V = a b [1,2 - 2,1 + 2 1 - 1 2] V la expresin obtenida para hacerla vlida usando lneas coordenadas generalizadas xp y xq en un espacio N-dimensional, obtenemos lo siguiente: V = a b [p,q - q,p + q p - p q] V Si la longitud en el recorrido a lo largo de una de las dos coordenadas utilizadas para el viaje del vector V es aumentado en un factor de dos, esto tambin aumenta el rea del parche de coordenadas ab en un factor de dos, doblando el valor de V. Esto significa que Vdepende linealmente de (a)ep y de (b)eq (aqu ep y eq son los vectores unitarios de base tangentes a las lneas de coordenadas seleccionadas para llevar a cabo el viaje), y obviamente tambin depende del 4-vector V. Si tomamos el trmino entre parntesis y lo definimos como: R = , - , + - entonces tenemos los componentes de un tensor R al cual si se le suministran como
argumentos el vector V (o mejor dicho, los componentes V del vector V a travs del ndice ) as como (a)ep, y de (b)eq a travs de los ndices y nos proporcionar V, el cambio en el componente del vector V cuando se le aplica una operacin de transporte paralelo sobre una trayectoria en una superficie curva. Esto es precisamente lo que nos fija geomtricamente el tensor de Riemann. Problemas PROBLEMA: Demostrar la segunda identidad de Bianchi: R; + R; + R; = 0 Tomando la relacin correspondiente al tensor de Riemann de primer gnero: R = (g, - g, + g, - g,)/2 y llevando a cabo la diferenciacin ordinaria con respecto al parmetro tenemos lo siguiente: R, = (g, - g, + g, - g,)/2 De esta relacin, usando el hecho de que el tensor mtrico g es simtrico ( gab = gba) y el hecho de que las derivadas parciales ordinarias conmutan, obtenemos la segunda identidad de Bianchi. PROBLEMA: Sabiendo de antemano que en una 2-superficie la curvatura RiemannianaGaussiana K est definida de la siguiente manera:
siendo g el determinante del tensor mtrico g, obtener la expresin correspondiente a Kpara la siguiente mtrica:
Del elemento de lnea ds obtenemos los siguientes componentes que corresponden al tensor mtrico g: g11 = 1/(x1) ___g22 = 1/(x1) g12 = g21 = 0
as como los siguientes componentes que corresponden al tensor mtrico conjugado g-1: g11 = (x1) ___g22 = 1/(x1) g12 = g21 = 0 Con esto podemos obtener los smbolos de Christoffel que nos permitirn obtener al componente del tensor de Riemann que estamos buscando, R1212. Cuando los tres ndices del smbolo de Christoffel son iguales como en el caso de 111, tenemos que recurrir a la relacin explcita sin haber atajos posibles: = g (- g, + g, + g,)/2 = g (- g/x + g/x + g/x)/2 Entonces: 111 = g11 (- g11/x1 + g11/x1 + g11/x1)/2 111 = {(x1) } {g11/x1}/2 111 = {(x1) } {- 2 (x1) -3}/2
Empezamos con la evaluacin de 122:
A continuacin llevamos a cabo la evaluacin del smbolo de Christoffel 221 que por la
propiedad de simetra de los smbolos de Christoffel de segundo gnero es igual a 212:
Como no requerimos el smbolo de Christoffel 222 para la obtencin de R1212, no se llevar a cabo aqu la evaluacin del mismo. Para la obtencin de R1212 utilizamos la relacin general que nos d los componentes del tensor de Riemann: R = , - , + - la cual en este caso se nos convierte en: R1212 = 122,1 - 121,2 + 11 22 - 12 21 R1212 = 122/x1 - 121/x2 + 11 22 - 12 21 La evaluacin detallada se muestra a continuacin:
En cuanto al determinante del tensor mtrico, g, este ser: g = g11 g22 - g12 g21 Siendo g12 = g21 se tiene entonces: g = g11 g22 - (g12) La evaluacin de la curvatura K en base a la frmula dada es la siguiente:
Finalmente:
Esta curvatura no depende de las coordenadas, y por lo tanto la superficie descrita por esta mtrica es una superficie de curvatura constante. Una curvatura igual a cerocorresponde a la curvatura de una superficie plana. Una curvatura positiva constante corresponde a una superficie como la de la esfera. Y una superficie de curvatura negativa constante corresponde a algo como un hiperboloide. En el espacio-tiempo de 4 dimensiones, de las 20 componentes del tensor de Riemann la esencia de diez de ellas es capturada por el tensor de Ricci obtenido mediante una contraccin del tensor de Riemann que ser discutida posteriormente, mientras que la esencia de las diez restantes es capturada por otro tensor conocido como el tensor de Weyl:
Los tensores de Ricci y Einstein I vamos a construir una nueva teora en la cual sepultaremos definitivamente a la ley de la gravitacin universal de Newton -basada en la nocin de una fuerza invisible de atraccin entre los cuerpos- reemplazndola por algo en lo que conceptualmente habr una curvatura en el espacio-tiempo cuatri-dimensional causada por la presencia de masa-energa en cierta regin: curvatura geomtrica = densidad de masa-energa y si este concepto ser enunciado de modo tal que ser independiente del sistema de coordenadas empleado para describirlo, entonces habiendo estado expuestos al tensor de curvatura de Riemann nuestra primera ocurrencia tal vez ser emplearlo directamente en una igualdad tensorial como la siguiente: R = kT en donde k es una simple constante de proporcionalidad (como 8). El problema con este primer intento es que siendo el tensor de Riemann un tensor de orden cuatro la igualdad tensorial requerira que el tensor energa-tensin T fuera tambin de orden cuatro. Pero ya vimos que para nuestros propsitos un tensor energa-tensin T de orden dos parece ser suficiente. Entonces, ms que estirar a T convirtindolo en un tensor de orden cuatro, optaremos por convertir al tensor de curvatura de Riemann en otro tensor de curvatura de orden dos derivado de R, siempre y cuando no estemos sacrificando algo importante. Y lo primero que se nos viene a la mente es llevar a cabo una contraccin tensorial del tensor de Riemann igualando dos de sus ndices, lo cual lo convierte en un tensor de orden dos. Esto es precisamente lo que se logra con el tensor de Ricci. El tensor de Ricci es un tensor que se obtiene directamente del tensor de Riemann por una contraccin de dos de sus ndices. La eleccin del ndice covariante a contraer no es fija (se aprovecha aqu la ocasin para recordar que el proceso de contraccin activa automticamente la convencin de sumacin para ndices repetidos). La contraccin se lleva a cabo entre el ndice superior y el segundo ndice inferior del tensor de Riemann.
Al llevar a cabo una contraccin del tensor de Riemann, perdemos dos de los cuatro ndices que especifican a los componentes de dicho tensor de curvatura. Por qu razn es suficiente un tensor de dos ndices para describir el efecto -sobre el movimiento de los cuerpos- de la curvatura causada Partiendo de la definicin del tensor de Riemann, el cual es un tensor de orden cuatro, contravariante de orden uno y covariante de orden 3: R = , - , + - si llevamos a cabo una contraccin del primer ndice y el tercer ndice (el ndice superior y el segundo ndice inferior), obtenemos el siguiente tensor covariante de orden dos: R = R11 + R22 + R33 + R44 = R que est definido precisamente como el tensor de Ricci. El tensor de Ricci era el tensor favorito de Einstein, esto en virtud de que la definicin del tensor G de Einstein para formalizar matemticamente la curvatura en el espacio-tiempo que se nos manifiesta como la gravedad depende directamente del tensor de Ricci. l fue el primero en darse cuenta de la importancia de ese tensor para la construccin de una teora de la gravedad. Encontrar soluciones a la ecuacin fundamental de la Relatividad General equivale a buscar el tensor de Ricci que est asociado con la solucin. En la siguiente fotografa tenemos a Einstein en una visita famosa que hizo a Mount Wilson para agradecerle personalmente a Edwin Hubble su descubrimiento astronmico que permiti abandonar el modelo del Universo esttico por un Universo inflacionario en expansin:
En esta fotografa Einstein escribi en el pizarrn lo siguiente: Rik = 0 ? El signo de interrogacin que puso Einstein a la derecha de la expresin indica las dudas personales que ya albergaba sobre el modelo del Universo esttico al cual se haba aferrado y por el cual introdujo en su ecuacin tensorial la constante cosmolgica que tiempo despus llamara el error (intelectual) ms grande de su vida. Al presentar al mundo sus ecuaciones de campo, Einstein hizo la suposicin central de queen el espacio vaco el tensor de Ricci tiene un valor de cero: R = 0 Esta expresin constituye esencialmente la ley de gravitacin universal de Einstein. Una vez que tenemos el tensor covariante de Ricci R, aplicndole a dicho tensor con la ayuda de un tensor mtrico g contravariante una contraccin sobre sus dos ndices obtenemos un escalar R (un tensor de orden cero) conocido como el escalar de Ricci: R = gR
el cual viene siendo a fin de cuentas el resultado de una doble contraccin llevada a cabo sobre el tensor de Riemann: R = gR = g gR Con el tensor de Ricci en nuestras manos, nuestro primer intento en construr una nueva teora fsica con los tensores R = (R) y T = (T) parecera estar solucionado. Con los dos tensores de orden dos la curvatura geomtrica del espacio-tiempo puede ser igualada con la presencia de la masa-energa que produce dicha curvatura. Esto fue precisamente lo que hizo Einstein. Pero las primeras aplicaciones no slo produjeron resultados poco satisfactorios, sino inclusive contradictorios. La teora correcta para describir la nueva realidad fsica requera una modificacin del tensor de Ricci. El nuevo tensor construdo modificando el tensor de Ricci result ser precisamente el tensor de Einstein definido de la siguiente manera:
Resulta claro que el tensor de Einstein G es esencialmente un tensor mixto de orden dos, y la diferencia entre el tensor de Ricci R y el tensor de Einstein G se observa con mayor claridad viendo la representacin matricial de los componentes del tensor de Einstein:
La nica diferencia entre el tensor de Einstein y el tensor de Ricci estriba en la diagonal principal, a la cual se le resta a cada uno de sus componentes la mitad del escalar de Ricci. Esta parece una diferencia mnima. Y sin embargo, es justo lo que se requiere para que la ecuacin tensorial de la Relatividad General pueda ser utilizada para analizar y predecir fenmenos fsicos reales.
Puesto que el tensor de Ricci es un tensor simtrico, y puesto que el tensor de Einstein lo nico que hace es modificar las entradas en la diagonal principal, el tensor de Einstein tambin es un tensor simtrico. El tensor de Einstein G posee una propiedad importante: es un tensor libre de divergencia.
En general, en notacin tensorial compacta: G=R-gR Significado geomtrico de los tensores de curvatura
Un punto (0D) no puede tener ninguna curvatura. Una lnea (1D) slo puede tener curvatura externa: No hay lazo largo de la cual se puede transportar paralelo. La curvatura externa de una lnea se puede caracterizar por la radio local en un punto. 2D es el espacio de dimensin ms baja que puede tener curvatura interna. El ejemplo de superficie esfrica que hemos utilizado es un caso muy sencillo. Tiene el mismo radio en cada direccin en cada punto. Para obtener ms superficie curva general que tenemos diferentes radios en diferentes direcciones en un punto como en el caso de un elipsoide por ejemplo. Sin embargo, una radio es algo que se puede hablar de desde un punto de vista externo. Internamente slo podemos hablar de los resultados de un transporte paralelo en torno a un pequeo paralelogramo. En 2D, el original y los vectores son devueltos tanto en el plano tangente en el punto. La longitud del vector no cambia durante el transporte paralelo, de modo que el vector devuelto puede diferir de la original slo por el ngulo entre ellos. Se puede demostrar que este ngulo no depende de lo paralelogramo que elegir, pero slo en el rea de la misma. As, toda la informacin acerca de la curvatura interna de una superficie 2D en un punto dado puede ser descrito por un solo nmero .En geometra diferencial escalar de Ricci nos puede decir todo acerca de la curvatura de una superficie 2D. Todos los 4 componentes del tensor de Ricci 2D y los 16 componentes del tensor de Riemann 2D se puede calcular a partir de este escalar nico.
You might also like
- Numeros PDFDocument110 pagesNumeros PDFJhan Carlos Bran ReyesNo ratings yet
- Numeros PDFDocument110 pagesNumeros PDFJhan Carlos Bran ReyesNo ratings yet
- PPP DionisioDocument30 pagesPPP DionisioJhan Carlos Bran ReyesNo ratings yet
- Laboratorio N°1-Difraccion de Rayos XDocument5 pagesLaboratorio N°1-Difraccion de Rayos XJhan Carlos Bran ReyesNo ratings yet
- Auditoria FinancieraDocument10 pagesAuditoria FinancieraJhan Carlos Bran ReyesNo ratings yet
- Libro de Cepre de FisicaDocument13 pagesLibro de Cepre de FisicaJhan Carlos Bran ReyesNo ratings yet
- Aritmética Compendio Académico UNFV-CEPREVIDocument156 pagesAritmética Compendio Académico UNFV-CEPREVItavito_1250% (2)
- QUIMICA IntegralDocument221 pagesQUIMICA Integraljohnny palominoNo ratings yet
- Semana 1Document99 pagesSemana 1Daniel GallegosNo ratings yet
- FísicaDocument160 pagesFísicaJampier ríos CáceresNo ratings yet
- QUIMICA IntegralDocument221 pagesQUIMICA Integraljohnny palominoNo ratings yet
- Descentralización Educativa en el Perú: Distinciones ConceptualesDocument38 pagesDescentralización Educativa en el Perú: Distinciones ConceptualesJhan Carlos Bran ReyesNo ratings yet
- Rentas de Trabajo 4ta y 5taDocument71 pagesRentas de Trabajo 4ta y 5taJhan Carlos Bran ReyesNo ratings yet
- 2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Document5 pages2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Juan Alejandro Rosales CoronelNo ratings yet
- Descentralización Educativa en el Perú: Distinciones ConceptualesDocument38 pagesDescentralización Educativa en el Perú: Distinciones ConceptualesJhan Carlos Bran ReyesNo ratings yet
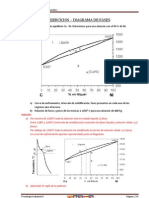
- Ejercicios Resueltos Diagrama de Fases - Daniel Gomariz - Ingeniería IndustrialDocument20 pagesEjercicios Resueltos Diagrama de Fases - Daniel Gomariz - Ingeniería IndustrialDaniel Gomariz63% (8)
- 2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Document5 pages2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Juan Alejandro Rosales CoronelNo ratings yet
- 2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Document5 pages2003 - Matematica 2 Et3 - Modelo - 201521 - 201521Juan Alejandro Rosales CoronelNo ratings yet
- Fundamentos de QuímicaDocument29 pagesFundamentos de QuímicaThania María SolorzanoNo ratings yet
- ProyectoDocument32 pagesProyectoJhan Carlos Bran ReyesNo ratings yet
- Boylestad Robert L - Electrónica Teoría de Circuitos 6° Edición PDFDocument655 pagesBoylestad Robert L - Electrónica Teoría de Circuitos 6° Edición PDFapi-370188485% (13)
- Informe de Mecánica de SuelosDocument33 pagesInforme de Mecánica de SuelosJhan Carlos Bran ReyesNo ratings yet
- Circuitos Electronicos PracticosDocument21 pagesCircuitos Electronicos PracticosgatobbaNo ratings yet
- 3cera Edi 5 Quimica III UltimoDocument132 pages3cera Edi 5 Quimica III UltimosaulotejadaNo ratings yet
- COBREcorrosion AleacionesDocument73 pagesCOBREcorrosion Aleacioneswildor_sanchezNo ratings yet
- 12metamateriales Expo de OpticaDocument20 pages12metamateriales Expo de OpticaJhan Carlos Bran ReyesNo ratings yet
- Ejercicios Resueltos Diagrama de Fases - Daniel Gomariz - Ingeniería IndustrialDocument20 pagesEjercicios Resueltos Diagrama de Fases - Daniel Gomariz - Ingeniería IndustrialDaniel Gomariz63% (8)
- Impri Mir Cruc IsDocument8 pagesImpri Mir Cruc IsJhan Carlos Bran ReyesNo ratings yet
- Circuitos en Corriente ContinuaDocument51 pagesCircuitos en Corriente ContinuaJhan Carlos Bran ReyesNo ratings yet
- Preguntas para El Simulacro2vDocument7 pagesPreguntas para El Simulacro2vJhan Carlos Bran ReyesNo ratings yet
- Calculo Diferencial - Álvaro Pinzón PDFDocument312 pagesCalculo Diferencial - Álvaro Pinzón PDFLioAldair Madden Miranda100% (19)
- SILABODocument14 pagesSILABOLUZ YANINA MAURICIO HUAMANINo ratings yet
- Apuntes Ec DiferencialesDocument260 pagesApuntes Ec DiferencialesEsaú E Rodriguez100% (1)
- Matematica Aplicada 2Document7 pagesMatematica Aplicada 2Dominguez Bernal Carmen ElizabethNo ratings yet
- Solución parcial cálculo diferencial UdeMDocument6 pagesSolución parcial cálculo diferencial UdeMAndres Sebastian Sosa AcevedoNo ratings yet
- Proyecto de Grado Camila GonzalezDocument5 pagesProyecto de Grado Camila Gonzalezkamilagonza5358No ratings yet
- Aplicacion de Las Derivadas en El Mundo RealDocument2 pagesAplicacion de Las Derivadas en El Mundo Realahnjaewook_10No ratings yet
- Solucion Interrogacion 1Document6 pagesSolucion Interrogacion 1Matias NicolasNo ratings yet
- Funciones de Varias VariablesDocument32 pagesFunciones de Varias VariablesKcc J.No ratings yet
- Egc 201 Matematica IiDocument5 pagesEgc 201 Matematica IijuniorNo ratings yet
- Protocolo Individual 2 Calculo VectorialDocument7 pagesProtocolo Individual 2 Calculo Vectorialkarin perezNo ratings yet
- Herodoto. Los Nueve Libros de La Historia Tomo IDocument545 pagesHerodoto. Los Nueve Libros de La Historia Tomo ILuis IvanNo ratings yet
- CALCULO DIFERENCIAL Jessik Mendoza PDFDocument207 pagesCALCULO DIFERENCIAL Jessik Mendoza PDFdonklanklaNo ratings yet
- Analisis Cualitativo de Un Modelo de CompetenciaDocument15 pagesAnalisis Cualitativo de Un Modelo de CompetenciaRenzo Osmar Salazar CarazasNo ratings yet
- Derivadas de Funciones de Varias VariablesDocument12 pagesDerivadas de Funciones de Varias VariableskarenNo ratings yet
- Silabo Calculo 1 2020 1Document3 pagesSilabo Calculo 1 2020 1Fátima VelasquezNo ratings yet
- PROYECTO DE CALCULO Final Presentar PDFDocument36 pagesPROYECTO DE CALCULO Final Presentar PDFEddie AlarconNo ratings yet
- Optimización de FuncionesDocument17 pagesOptimización de FuncionesFarid J OrtizNo ratings yet
- Apuntes EdoDocument209 pagesApuntes EdoCarmenRadoiNo ratings yet
- Unidad IVDocument23 pagesUnidad IVCasual NetworkNo ratings yet
- Regla de La Cadena, Derivada Implícita y Derivada de Orden Superior +++Document49 pagesRegla de La Cadena, Derivada Implícita y Derivada de Orden Superior +++FJ oloyagNo ratings yet
- Matematica IIDocument2 pagesMatematica IIM4Gn3tONo ratings yet
- Notas de Análisis Real - Eugenio P. BalanzarioDocument144 pagesNotas de Análisis Real - Eugenio P. BalanzarioRoberto CarlosNo ratings yet
- Derivadas Parciales EjerciciosDocument14 pagesDerivadas Parciales EjerciciosK Mendez Leon100% (2)
- Fases y EnvolventesDocument10 pagesFases y EnvolventesNixon AyalaNo ratings yet
- Encuadre Calculo Diferencial 2022 - 080440Document5 pagesEncuadre Calculo Diferencial 2022 - 080440Roberto AlvaroNo ratings yet
- TALLERNo1 (Inte - Ind.2023 A)Document5 pagesTALLERNo1 (Inte - Ind.2023 A)Luis LPNo ratings yet
- Proyecto de Tesis FinalDocument15 pagesProyecto de Tesis FinalJoaquin PabloNo ratings yet
- 17-Texto Del Artículo-66-1-10-20200219Document7 pages17-Texto Del Artículo-66-1-10-20200219Steph WolffNo ratings yet
- Ecuaciones Diferenciales PDFDocument10 pagesEcuaciones Diferenciales PDFAntonio Morocho RoseroNo ratings yet