THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS November 2012

MATH2130 Higher Mathematical Methods for Dierential Equations

(1) TIME ALLOWED 2 Hours (2) TOTAL NUMBER OF QUESTIONS 4 (3) ANSWER ALL QUESTIONS (4) THE QUESTIONS ARE OF EQUAL VALUE (5) THIS PAPER MAY BE RETAINED BY THE CANDIDATE (6) ONLY CALCULATORS WITH AN AFFIXED UNSW APPROVED STICKER MAY BE USED

All answers must be written in ink. Except where they are expressly required pencils may only be used for drawing, sketching or graphical work.

November 2012

MATH2130

Page 2

Information
Bessel equation
The Bessel equation of order is z 2 u + zu + (z 2 2 )u = 0 and has the general solution u(z ) = AJ (z ) + BY (z ), where

J (z ) =
k=0

(1)k (z/2)2k+ , k !(k + + 1)

J (z ) cos( ) J (z ) , = integer, sin( ) Yn (z ) = lim Y (z ), n = integer. Y (z ) =

n

If Re > 0, then Y (z ) D z as z 0, for a nonzero constant D . If is not equal to a negative integer, then J (z ) C z as z 0, for a nonzero constant C .

Please see over . . .

November 2012 1. i) Solve 2(cos2 x)y

MATH2130

Page 3

dy y 2 = 1, dx

y (0) = 2.

ii) Use variation of parameters to nd a particular solution u = u(x) of x 4u + u = tan2 . 2 You may assume that 2 d 1 + sin = log . cos d 1 sin iii) Use the Frobenius method to construct a solution of 6z 2 u + 7zu + (2z 1)u = 0 such that u(z ) is bounded as z 0. Show explicitly the rst three terms in the series expansion of u. 2. i) Find the general solution of the inhomogeneous CauchyEuler ODE x3 u + 3x2 u 2xu + 2u = 6x1 . ii) a) Show that if u1 and u2 are any solutions of the ODE a2 (x)u + a1 (x)u + a0 (x)u = 0, then their Wronskian W satises a2 (x)W + a1 (x)W = 0. b) Hence determine the form of the Wronskian of any two solutions of the Legendre equation (1 x2 )u 2xu + ( + 1)u = 0. iii) Consider the dierential operator Lu = u + 2(cos x)u ex u. a) Find L , the formal adjoint of L. b) Suppose that u(0) + u (0) = 0 and u(/2) = 0. Determine boundary conditions for v that ensure
/2 /2

(Lu) v dx =
0 0

u L v dx.

Please see over . . .

November 2012

MATH2130

Page 4

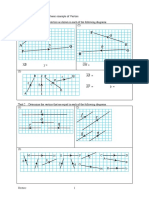
Figure 1: Solutions of the equation (1).

3. Let Lu = (xu ) + x1 u, and consider the SturmLiouville problem Lu = xu for 1 < x < 2, with u(1) = 0 = u(2). i) Prove that every eigenvalue of L is strictly positive. (You may assume 2 that must be real.) Hint: consider 1 u Lu dx. ii) Find the general solution of Lu = xu if = k 2 . iii) Hence show that = k 2 is an eigenvalue i k satises J1 (k )Y1 (2k ) Y1 (k )J1 (2k ) = 0. (1)

iv) Assume that (1) has a sequence of positive solutions 0 < k1 < k2 < (as shown in Figure 1). Write down an eigenfunction j corresponding 2 to the eigenvalue j = kj . v) State the orthogonality property of the eigenfunctions. vi) Consider a boundary value problem Lu xu = f for 1 < x < 2, with u(1) = 0 = u(2).

a) If the case when is not an eigenvalue, give a formula for the generalized Fourier coecient Aj in the expansion

u(x) =
j =1

Aj j (x).

b) When = j , what condition must f satisfy in order for a solution u to exist? Write down the form of u if this condition holds. Please see over . . .

November 2012

MATH2130

Page 5

4. Consider an elliptic eigenproblem on the unit square: (xx + yy ) = x + a = 0 x = 0 y = 0 for for for for 0 < x < 1 and 0 < y < 1, x = 1 and 0 < y < 1, x = 0 and 0 < y < 1, y {0, 1} and 0 < x < 1,

where a is a positive constant and x = /x, xx = 2 /x2 , etc. i) Sketch the domain (0, 1) (0, 1), indicating the boundary conditions for each part of the boundary. ii) Use a graphical argument to show that the equation tan = a

has a sequence of positive solutions 0 < 0 < 1 < 2 < , with 1 ) for every j 0. j < j < (j + 2 iii) Use separation of variables, (x, y ) = X (x)Y (y ), to show that the eigenvalues are
2 jk = j + (k )2

for j = 0, 1, 2, . . . and k = 0, 1, 2, . . . ,

and nd the corresponding eigenfunctions jk (x, y ). iv) A long beam with a square cross-section is insulated on three of its faces. At t = 0, the beam is at a uniform temperature b, after which it begins to cool as heat radiates from the fourth (uninsulated) face. With the z -axis parallel to the beam, the temperature u = u(x, y, t) satises ut (uxx + uyy ) = 0 u=b ux + au = 0 ux = 0 uy = 0 for for for for for 0 < x < 1, 0 < y < 1 and t > 0, 0 < x < 1 and 0 < y < 1, when t = 0, x = 1 and 0 < y < 1, x = 0 and 0 < y < 1, y {0, 1} and 0 < x < 1,

where b is a positive constant. Find u.