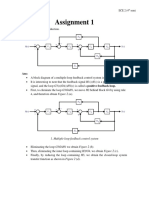
Professional Documents
Culture Documents
Chapter 7
Uploaded by
trushalvoraOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Chapter 7
Uploaded by
trushalvoraCopyright:
Available Formats
Modeling and Control of Dynamic Systems
MESB323
Chapter 7
Stability
7.1. Introduction
Stability is a very important aspect of control system. One of the main objectives of control
system is to achieve stability. If a system is not stable then the response will become
uncontrollable and the system will be unstable. In this topic we will learn about system stability
and how to determine whether a system is stable or unstable.
7.2. Definitions
There are two definitions of stability:
First Definition:
Based on total response of the system which we call 'Bounded Input Bound Output' (BIBO).
Second Definition:
Based on a natural response of the system due to initial condition.
Based on the first definition:
(a)
A Linear time invariant (LTI) system is considered to be stable if a bounded input yields
a bounded otput. Bounded mean the signal does not go out bounded.
(b)
A LTI system is considered to be unstable if a bounded input yields an unbounded
output. This mean the output goes beyond bound.
Based on the second definition:
(a)
A system is said to be stable, if the natural response of the system approaches zero as
time (t) approaches infinity ().
(b)
A system is said to be unstable if the natural response of the system approaches infinity
as time (t) approaches infinity ().
Let us examine the two cases below:
Recalling basic chapter 5, output response of system consists of two parts:
Forced response + natural responses
Modeling and Control of Dynamic Systems
MESB323
C(t) = Cf (t) + Cn (t)
Total response = forced response + natural response
(i)
Y ( s)
5
U (s) s 2
Transfer function
(pole is -2)
y(t) = output and u(t)= unit step input. The initial condition y(0) = 0.
1
Suppose u(t) =1, then U(s)= s ,then the output is
5
A
B
Y ( s)
s ( s 2) s s 2
y (t) = A + B e- 2t
Force response
Natural response
2 t
As t , Be 0 . Alternatively, output y(t) is bounded and the unit step input u(t) is also
bounded. Hence the system is stable.
(ii) Transfer function
Y ( s)
5
U (s) s 2
(pole is +2)
For the same input condition as in case (i),
y (t ) A Be 2t
The input u(t) is bounded but the output is unbounded due to positive exponential term e
Hence the system is unstable.
2 t
Case (i) above where as t , f (t ) 0 only happens if the closed loop poles of the system are
on the left half of the s plane, basically if the poles have negative real values.
Closed loop poles on the right half plane yields instability as shown in case (ii)
A system is stable if the closed loop poles are on the left hand half of the s-plane
7.3. Necessary Condition of Stability
The closed loop poles are all on the left half plane if the coefficients of the characteristic
equation are all present and having the same sign. Characteristic equation (C.E) is the
denominator of the closed loop system's transfer function. If the coefficients of the C.E are all
having the same sign it does not mean that all the poles are on the left half plane. On the other
Modeling and Control of Dynamic Systems
MESB323
hand, if the poles are on the left half plane then all the coefficients of the C.E must have the
same sign.
Modeling and Control of Dynamic Systems
MESB323
Example 7.1
For the closed loop transfer function given below, determine the stability of the system.
(a)
C (s)
5
3
R ( s ) 3s 2 s 2 3s 6
(b)
C (s)
5
3
R ( s ) 3s 2 s 2 3s 6
C (s)
5
3
2
(c) R ( s ) 3s 3s 3s 6
Solution:
3
2
(a) The C.E is (3) s (2) s (3) s (6) 0
All coefficients are positive
Since all coefficients are same sign then the system satisfies the necessary condition for stability.
However we cannot surely state that the system is stable without locating the closed loop
poles.
3
2
(b) The C.E is 3s 2s 3s 6 0
In this case all the coefficients are not the same sign as the coefficient for s2 is negative
whereas all the other coefficients are all positive. Therefore this system does not satisfy the
necessary condition and it is not a stable system.
(c)
C (s)
5
3
R ( s ) 3s 3s 6
3
The C.E is 3s 3s 6 0
In this case all the coefficients are having the same sign but not all the coefficients are
present.
Coefficient for s2 is 0, therefore this is not a stable system. In order to check for stability, we
need to find the exact location of the closed loop poles. It is easy to find if the characteristic
equation is in the order of 2 or 3. However, it is very tedious when it comes to higher order
equation. In this case Routh-Hurwitz Criterion becomes very useful.
7.4. Routh-Hurwitz Criterion
Routh-Hurwitz Criterion states that, the roots of the equation are all in the left half plane (LHP)
if all the elements of the first column of the Routh's tabulation are having the same sign. The
number of sign changes in the first column of the Routh table equals to the number of roots with
positive real parts on the right half plane (RHP).
Modeling and Control of Dynamic Systems
MESB323
Routh's Table:
Let the transfer function of closed loop system be T(s) where
T (s)
as c
b4 s b3 s b2 s 2 b1 s1 b0
4
The characteristic equation in this case:4
3
2
1
C.E = b4 s b3 s b2 s b1s b0 = 0
(a) Start a column with the highest power of s in the C.E to s0.
s4
s3
s2
s1
s0
Table 7.1
(b) Fill the first row starting with the coefficient of the highest power of s followed by every
other coefficient in the C.E equation.
b4
s4
b2
b0
s
s2
s1
s0
Table 7.2
(c) Do the same for the next row starting with next highest power of s.
b4
b3
b2
b1
b0
0
a1
a2
a3
a4
a7
s
No more coefficients
a5
a8
a6
a9
s4
s
s2
s1
Modeling and Control of Dynamic Systems
MESB323
Table 7.3
(d) Each entries of the column are actually the negative determinant of entries in the previous
two rows divided by the entry in the first column directly above the calculated row.
The left hand column of the determinant is always the first column of the two previous
rows.
The right hand column of the determinants is the elements column above and to the
right.
s4
s
b4
b3
s2
a1
s1
s0
b0
0
b2
b1
b4
b3
b2
b1
a2
b3
b3 b1
b b
1 2
a1
a4
a1 a2
a
0
4
a5
a4
b4
b3
b0
0
b3
b4 0
b 0
3
0
a3
b3
b3 0
a 0
1
0
a5
a1
b3 0
a 0
1
0
a6
a1
a1 0
a 0
4
0
a6
a4
a1
a4
a7
0
0
0
Table 7.4
Note: To find the determinant, we do a cross multiply as shown below:
b b
b b
a
b
b b b b
a
b
b b b b
b
4
Example 7.2
Given a closed loop transfer function:
3s 1
T (s) 3
s 4s 2 s 6
(a)
Indicate how many poles are on the right half s plane and how many poles are on the left
half plane.
(b)
Is the system stable?
6
Modeling and Control of Dynamic Systems
MESB323
Solution:
The characteristic equation:
CE = s3- 4s2 + s + 6 =0
By observation, we know that the system is unstable as the coefficients of the C.E are not having
the same signal. First we solve it the normal way where we locate the closed loop poles and then
we will verify this with Routh Hurwitz method. In this case we can do both ways as the order of
the C.E is only 3.
Setting C. E = 0 (We can locate the closed loop poles)
s3 -4s2 + s + 6 = (s - 2)(s + 1)(s - 3)=0
Therefore the poles are at
s = 2, s = -1 and s = 3
There are two poles on the right half s plane and one pole on the left half s-plane. This system is
definitely unstable.
Second Method: Routh Hurwitz Method
C.E=s3-4s2+s+6 =0
s3
s2
s1
s0
1
-4
a1=2.5
b1=6
1
6
a2=0
0
Table 7.5
Basically the table will be
s3
s2
s1
s0
1
-4 (1st sign change)
2.5 (2nd sign change)
6
1
6
0
Table 7.6
Routh Hurwitz criterion states the number of sign changes in the first column of the Routh
table indicates the number of poles on the right half s- plane. In the table above we can
observe there are two sign changes. Therefore there are two poles on the right half s plane and
another pole is on the left half s-plane. This is the same result that we found by solving the C.E
to obtain the closed loop poles. This system is unstable
Modeling and Control of Dynamic Systems
MESB323
Example 7.3:
Given the closed loop transfer function of a system is T(s) where
3s 5
2
T(s) = 4 s 2 s 6 s 10 s 20
4
(i)
Indicate how many poles on the right half s plane and how many poles on the left half s
plane.
(ii)
Indicate whether the system is stable or unstable.
Simplified the table will be: Two sign change
4
2
-14
90
7
20
s4
s3
s2
s1
s0
6
10
20
0
20
0
Table 7.8
(a)
From the Table 7.8, we can see that there are two sign changes therefore 2 poles on
the right half s-plane. Since this system supposed to have 4 poles (the denominator of
the system is 4th order) the other two poles are on the left half s plane.
(b)
The system is unstable as the system has poles on the right half s-plane.
7.3.1
Special Cases for Routh Table
There are two special cases that we need to consider while tabulating the Routh table.
1. The first element in anyone row of Routh's table is zero but others are not.
This case will be explained using Example 7.4
Example 7.4:
Given the closed loop transfer of a system
T (s)
2 s 2 3s 4
s 4 s 3 4s 2 4s 3
(a) Tabulate the Routh table.
(b) Find how many poles are on the right half s-plane and how many poles on the left half
s-plane.
8
Modeling and Control of Dynamic Systems
MESB323
Solution:
(a)
CE = s4 +s3 +4s2 +4s+3
s4
s3
s2
s1
1
1
1(4 4)
a1
0
1
(3 0)
b1
0
?
4
4
(0 3)
a2
3
1
s0
Table 7.9
As we can see in the table above, the value of bl is undefined as a1 is zero. For cases like this
above where the first element in any one row is zero, the table can be completed by a replacing a
very small value which is called epsilon (). This can be taken as a very small positive value or
a very small negative value.
(b)
(very small positive value)
s4
s3
s2
s1
1
1
s0
(3 4 )
4
4
3
0
3
0
Table 7. 10
Since is a very small positive value, the sign in the first row of Table 6.10 is
+
s4
3
+
s
2
+
s
1
s
0
+
s
1 sign change
2 sign change
Table 7. 11
3
0
Modeling and Control of Dynamic Systems
MESB323
(a)
From the table above, the two sign changes. Therefore there are two poles on the right
half s-plane and two poles on the left half s-plane. We will get the same result if we take
to be a very small negative value as shown below.
(b)
(very small negative value)
+
+
+
+
s4
s3
s2
s1
s0
Table 7.12
The results are just the same as in (ii) where a positive small value is used.
2. The second special case occurs when all elements in a row are zeros.
This indicates one or more of the following conditions:
(a) The equations has one pair of real roots with equal magnitude but opposite signs.
(b) The equation has one or more roots on the imaginary axis.
(c) The equation has complex conjugate roots forming symmetry at the origin.
Example 7.5:
Given a closed loop transfer function of a system
T (s)
203s
s s 10s 10 s 2 169 s 169
5
(a) Tabulate the Routh table.
(b) Indicate the location of the closed loop poles solution.
Solution:
5
4
3
2
(a) CE = s s 10 s 10s 169s 169
10
Modeling and Control of Dynamic Systems
s5
s4
s3
s2
s1
s0
1
1
0
MESB323
10
10
0
169
169
0
All element in the row are zero
Table 7.13
The situation with all zeros in the row like above is solved using auxiliary equation of P(s) = 0.
Auxiliary equation P(s) is formed from the coefficients of the row just before the row of zeros in
the Routh tabulation. For this case the row above the row of zeros have coefficient 1 for s4, 10
for s2 and 169 for s0.
Therefore:
P(s) = s4 + 10s2 +169s0
Take the differentiation of P(s) with respect to s
dP ( s )
4 s 3 20s 0
ds
dP ( s )
The coefficients of ds are filled replacing the row of zeros and the other elements are found
like usual using these values.
s5
s4
s3
s2
s1
s0
1
1
4
5
-115.2
169
10
10
20
169
11
169
169
Modeling and Control of Dynamic Systems
MESB323
Table 7.14
(b) For this case, we have two consider the tables in two different parts in determining the
location of the closed loop transfer function. The first part will be from the beginning of the
table till the row before the row of zeros (ROZ). The second part will be a test of even
polynomial from the row before the row of zeros (ROZ) till the end of the table.
(i) For the first part we have:
+
+
s5
s4
1 pole
*Note this is order 1 as only 1 pole
Table 7.15
There are no sign changes indicating 1 pole on the left hand side of the s-plane.
12
Modeling and Control of Dynamic Systems
MESB323
The second part, we have
s4
s3
s2
s1
s0
1 pole
2 pole
3 pole
4 pole
+
+
+
+
Note: This is order
four so there are 4
poles with
2 sign changes
Table 7.16
In this case there is 2 sign changes indicating 2 poles of the right hand side of the 2-plane and 2
poles on the left hand side of the s-plane because of the requirement of symmetry. Basically we
can summarize in a table form as shown below:
Location
Other
Order 1
0
1
0
Right hand side
Left hand side
Even
Fourth Order
2
2
0
Total
Fifth Order
2
3
0
Table 7.17
The system is unstable since there are two poles on the right hand side of the s-plane.
Note: If there are no sign changes in the second part then there is no poles on the right half plane
which means there are no poles on left half plane as well (symmetry condition). Therefore all
the 4 poles will be on the imaginary axis.
13
You might also like
- AssignmentsDocument22 pagesAssignmentsanshNo ratings yet
- Stability Analysis Using Routh-Hurwitz CriterionDocument34 pagesStability Analysis Using Routh-Hurwitz CriterionNina ButtNo ratings yet
- Stability of Linear Systems: DR K P Mohandas, Professor, NIT CalicutDocument7 pagesStability of Linear Systems: DR K P Mohandas, Professor, NIT Calicutsuresh1virdiNo ratings yet
- Experiment No 1 Analysis of Control System ParametersDocument6 pagesExperiment No 1 Analysis of Control System Parameterspratik KumarNo ratings yet
- Lecture 14, 15 StabilityDocument45 pagesLecture 14, 15 StabilityHamza KhanNo ratings yet
- Lab 08 PDFDocument10 pagesLab 08 PDFAbdul Rehman AfzalNo ratings yet
- Stability Analysis MATLABDocument10 pagesStability Analysis MATLABSohail Afridi100% (1)
- Linear Algebra HW1Document4 pagesLinear Algebra HW1Gomi9kNo ratings yet
- Lecture 14 StabilityDocument26 pagesLecture 14 StabilityHamza KhanNo ratings yet
- Analyzing Time Domain ResponseDocument15 pagesAnalyzing Time Domain ResponseBasharat AslamNo ratings yet
- PDC Lecture Notes 7 - Stability of Closed-Loop Systems 2018Document56 pagesPDC Lecture Notes 7 - Stability of Closed-Loop Systems 2018R-A PascualNo ratings yet
- Stability: Oncept OF TabilityDocument9 pagesStability: Oncept OF TabilityPATEL KRISHNANo ratings yet
- pw3 SolDocument12 pagespw3 Soltwee tomasNo ratings yet
- Motor Drive With Flexible Shaft Control SystemDocument32 pagesMotor Drive With Flexible Shaft Control Systemعدي القهالي100% (2)
- 0 7 Lec7 EE418 Routh - Herwitz - Stability - CriterionDocument58 pages0 7 Lec7 EE418 Routh - Herwitz - Stability - Criterionyoussef hossamNo ratings yet
- Question Bank Linear Control SystemsDocument15 pagesQuestion Bank Linear Control SystemsarafatasgharNo ratings yet
- Prof. Eisa Bashier M.Tayeb 2021: Control System StabilityDocument18 pagesProf. Eisa Bashier M.Tayeb 2021: Control System StabilityOsama AlzakyNo ratings yet
- Control Systems U3 (TEL306)Document84 pagesControl Systems U3 (TEL306)Ruvenderan SuburamaniamNo ratings yet
- Control Systems Theory: Transient Response Stability STB 35103Document68 pagesControl Systems Theory: Transient Response Stability STB 35103Muhammad Irvan FNo ratings yet
- LIM_ACTIVITY7_FIRST-ORDER-SYSTEMDocument14 pagesLIM_ACTIVITY7_FIRST-ORDER-SYSTEMLIM, SHERYL M.No ratings yet
- Stabilty Routh HurwitzDocument57 pagesStabilty Routh Hurwitzjinto0007No ratings yet
- Linear Control Cheat SheetDocument13 pagesLinear Control Cheat SheetOmnia Hashad92% (13)
- Lecture Ruth Herwitz Stability CriterionDocument22 pagesLecture Ruth Herwitz Stability CriterionIslam SaqrNo ratings yet
- ELE 4623: Control Systems: Faculty of Engineering TechnologyDocument16 pagesELE 4623: Control Systems: Faculty of Engineering TechnologyMaitha SaeedNo ratings yet
- Introduction To Linear Control System PDFDocument13 pagesIntroduction To Linear Control System PDFAmitava BiswasNo ratings yet
- Transient and Steady State AnalysisDocument22 pagesTransient and Steady State AnalysisRajath UpadhyaNo ratings yet
- Time Domain Response and Control Characteristics: ObjectivesDocument11 pagesTime Domain Response and Control Characteristics: ObjectivesÃbdûł HãnñāńNo ratings yet
- Determine System Stability Using Routh-Hurwitz CriterionDocument28 pagesDetermine System Stability Using Routh-Hurwitz CriterionDaniel MengeshaNo ratings yet
- Adobe Scan Jan 05, 2023Document4 pagesAdobe Scan Jan 05, 2023Vennela VaddiNo ratings yet
- Chapter 6 System StabilityDocument32 pagesChapter 6 System StabilityIzzat AiresNo ratings yet
- Lecture 8 Routh Herwitz Stability CriterionDocument25 pagesLecture 8 Routh Herwitz Stability Criterionusama asifNo ratings yet
- StabilityDocument8 pagesStabilityGianco VillarrealNo ratings yet
- chapter-5Document78 pageschapter-5hailegebreselassie24No ratings yet
- Chap 5 - Routh Hurwitz Stability Criterion: UEEA 3423 Control SystemsDocument35 pagesChap 5 - Routh Hurwitz Stability Criterion: UEEA 3423 Control SystemsYap Win IanNo ratings yet
- EEE CONTROL SYSTEM Gate Questions: 40dB / Dec 80dB 60dB / DecDocument12 pagesEEE CONTROL SYSTEM Gate Questions: 40dB / Dec 80dB 60dB / Decnaveeth11No ratings yet
- Control Systems - Experiment 3Document16 pagesControl Systems - Experiment 3EnesVSNo ratings yet
- Chapter6 - Ver 1Document16 pagesChapter6 - Ver 1George MathaiNo ratings yet
- Routh-Hurwtz Criterion & Root-Locus Criteria: Stability of Feedback Control SystemsDocument19 pagesRouth-Hurwtz Criterion & Root-Locus Criteria: Stability of Feedback Control Systemsember_memoriesNo ratings yet
- ME375 Prelab 2Document7 pagesME375 Prelab 2Jason LeeNo ratings yet
- Control Ball Beam PositionDocument14 pagesControl Ball Beam PositionJorge PorrasNo ratings yet
- Gelb ch3 Ocr PDFDocument102 pagesGelb ch3 Ocr PDFbacuoc.nguyen356No ratings yet
- Stability of Linear Control System: Bounded-Input Bounded-Output (BIBO) StabilityDocument9 pagesStability of Linear Control System: Bounded-Input Bounded-Output (BIBO) Stabilitymeseret sisayNo ratings yet
- FeedCon (Unit 3)Document39 pagesFeedCon (Unit 3)engrwhoNo ratings yet
- Algebraic Criterion for StabilityDocument57 pagesAlgebraic Criterion for StabilityPhani Sarma NagavarapuNo ratings yet
- Closed-loop control system block diagramDocument41 pagesClosed-loop control system block diagramTing SamuelNo ratings yet
- Ee 469Document39 pagesEe 469arwa zeglamNo ratings yet
- ECNG-4010 Lecture 09Document28 pagesECNG-4010 Lecture 09Abel BatuNo ratings yet
- Control System Fundamental: Time Response AnalysisDocument77 pagesControl System Fundamental: Time Response Analysisoneisa92100% (1)
- Routh's Stability Criterion: A S A S A S A S ADocument3 pagesRouth's Stability Criterion: A S A S A S A S Afarhan_bahariNo ratings yet
- Slide 2Document89 pagesSlide 2EnesVSNo ratings yet
- Linear AlgebraDocument150 pagesLinear AlgebrameastroccsmNo ratings yet
- Q1: Put The Sign For Right Sentences and The Sign X For Wrong SentencesDocument18 pagesQ1: Put The Sign For Right Sentences and The Sign X For Wrong SentencesWaleed HåšhįmNo ratings yet
- Regulation and Control: by Tewedage SileshiDocument22 pagesRegulation and Control: by Tewedage SileshihermelaNo ratings yet
- Transfer Functions Block Diagrams Signal Flow Graph Mason's Gain FormulaDocument28 pagesTransfer Functions Block Diagrams Signal Flow Graph Mason's Gain FormulaMesut OzilNo ratings yet
- Old Question Paper Control SystemsDocument7 pagesOld Question Paper Control SystemsSatendra KushwahaNo ratings yet
- PD CONTROL FOR ROBOTIC MANIPULATORSDocument47 pagesPD CONTROL FOR ROBOTIC MANIPULATORSArdian Ramadita SugaraNo ratings yet
- 1 + 1 = 1 An Introduction to Boolean Algebra and Switching CircuitsFrom Everand1 + 1 = 1 An Introduction to Boolean Algebra and Switching CircuitsRating: 4 out of 5 stars4/5 (2)
- Reactive Oxygen Species: Signaling Between Hierarchical Levels in PlantsFrom EverandReactive Oxygen Species: Signaling Between Hierarchical Levels in PlantsFranz-Josef SchmittNo ratings yet
- Implementationplan Chris ConnorsDocument3 pagesImplementationplan Chris ConnorstrushalvoraNo ratings yet
- Implementationplan Chris ConnorsDocument3 pagesImplementationplan Chris ConnorstrushalvoraNo ratings yet
- Tutorial 2Document1 pageTutorial 2trushalvoraNo ratings yet
- Bill of MaterialsDocument1 pageBill of MaterialstrushalvoraNo ratings yet
- Mechanics of Materials Quiz 2 Questions SolvedDocument3 pagesMechanics of Materials Quiz 2 Questions SolvedtrushalvoraNo ratings yet
- Lab 2Document19 pagesLab 2trushalvoraNo ratings yet
- Final - MEHB223 S2 2013 2014 1Document16 pagesFinal - MEHB223 S2 2013 2014 1trushalvoraNo ratings yet
- Sustainability Report 2011Document96 pagesSustainability Report 2011trushalvoraNo ratings yet
- Bill of MaterialsDocument1 pageBill of MaterialstrushalvoraNo ratings yet
- Environmental EffectsDocument17 pagesEnvironmental EffectstrushalvoraNo ratings yet
- Second Order Natural Response ExamplesDocument13 pagesSecond Order Natural Response ExamplestrushalvoraNo ratings yet
- Power WordsDocument1 pagePower WordstrushalvoraNo ratings yet
- Force Dynamic: 5 (0 Cos 45) 5 (2) Sin 45 5 (0sin 45) 5 (2) Cos 45Document3 pagesForce Dynamic: 5 (0 Cos 45) 5 (2) Sin 45 5 (0sin 45) 5 (2) Cos 45trushalvoraNo ratings yet
- Mechanics of Materials Quiz 2 Questions SolvedDocument2 pagesMechanics of Materials Quiz 2 Questions SolvedtrushalvoraNo ratings yet
- Mehb221 - EXP 5Document9 pagesMehb221 - EXP 5trushalvoraNo ratings yet
- Power WordsDocument1 pagePower WordstrushalvoraNo ratings yet
- AsdasdaDocument1 pageAsdasdatrushalvoraNo ratings yet
- AsdqweqDocument2 pagesAsdqweqtrushalvoraNo ratings yet
- AsdasdaDocument1 pageAsdasdatrushalvoraNo ratings yet
- Kasturi SPM Seminar 2011Document12 pagesKasturi SPM Seminar 2011trushalvoraNo ratings yet
- MRC Tentative 2013 For GuestDocument2 pagesMRC Tentative 2013 For GuesttrushalvoraNo ratings yet
- Hinduism Question.Document1 pageHinduism Question.trushalvoraNo ratings yet
- Arduino Uno Solar CalculationsDocument6 pagesArduino Uno Solar CalculationsHoussem Eddine HassineNo ratings yet
- Tutorial SVM MatlabDocument113 pagesTutorial SVM MatlabVíctor Garrido Arévalo100% (1)
- Introduction To Measure Theoretic Probability 2nd Edition Roussas Solutions ManualDocument18 pagesIntroduction To Measure Theoretic Probability 2nd Edition Roussas Solutions Manualyvonnewelchdoafexwzcs100% (17)
- ACT Math Facts & FormulasDocument8 pagesACT Math Facts & Formulaslslisen100% (1)
- Discrete DistributionsDocument25 pagesDiscrete DistributionsMuhammad Asad SheikhNo ratings yet
- Pre-Calculus: Updated 09/15/04Document14 pagesPre-Calculus: Updated 09/15/04Neha SinghNo ratings yet
- Factors and Multiples #NotesDocument12 pagesFactors and Multiples #NotesVijayalakshmi ISAMNo ratings yet
- 1st Term 2021 G10 P4 Maths OnlineDocument6 pages1st Term 2021 G10 P4 Maths OnlineMuhammadNo ratings yet
- Dynaminc OptimizationDocument399 pagesDynaminc OptimizationAlejandro Vazquez100% (2)
- Applied Probability and Statistics Unit I:Random VariablesDocument10 pagesApplied Probability and Statistics Unit I:Random VariablesBarath KumarNo ratings yet
- Two-Variable Regression Model, The Problem of EstimationDocument67 pagesTwo-Variable Regression Model, The Problem of Estimationwhoosh2008No ratings yet
- Quarter 1: Math 7 SummativeDocument4 pagesQuarter 1: Math 7 SummativeMailyn EpaNo ratings yet
- ECE 213 Unit 2Document37 pagesECE 213 Unit 2Bindu VangaNo ratings yet
- Problem:: Solve The Following LPP by Using Simplex Method. Subjected To ConstraintsDocument19 pagesProblem:: Solve The Following LPP by Using Simplex Method. Subjected To ConstraintsAffu ShaikNo ratings yet
- Advanced Control Using MatlabDocument541 pagesAdvanced Control Using Matlabboilerqwerty81100% (2)
- Mathematical Applications For The Management Life and Social Sciences 10th Edition Harshbarger Test Bank 1Document49 pagesMathematical Applications For The Management Life and Social Sciences 10th Edition Harshbarger Test Bank 1lynda100% (46)
- Quarterly Report On Rasa Basa ImplementationDocument2 pagesQuarterly Report On Rasa Basa ImplementationJonathan Olegario100% (2)
- Answer Key - Final Exam - Math102-L02-Fall 2020-V1+V2Document10 pagesAnswer Key - Final Exam - Math102-L02-Fall 2020-V1+V2alwafa.q6rNo ratings yet
- Introduction To AlgebraDocument2 pagesIntroduction To AlgebraHNo ratings yet
- Mathpower 11, Western EditionDocument14 pagesMathpower 11, Western EditionJoJo IsthewayNo ratings yet
- Lumen OhmDocument9 pagesLumen Ohmapi-388593380No ratings yet
- Curriculum: Bachelor of Science in Chemical Engineering (Bsche)Document5 pagesCurriculum: Bachelor of Science in Chemical Engineering (Bsche)LORIA DAGLINo ratings yet
- 0580 s12 QP 22Document12 pages0580 s12 QP 22Aryan RajputNo ratings yet
- Geometric Constructions and Their Arts in Historical Perspective - Reza SarhangiDocument11 pagesGeometric Constructions and Their Arts in Historical Perspective - Reza SarhangiAltanany100% (1)
- Technical Indicator Library Excel FormulaDocument30 pagesTechnical Indicator Library Excel FormulaAqeel AbbasNo ratings yet
- CH 04Document43 pagesCH 04Shashwat JhaNo ratings yet
- QT Notes 7 PDFDocument50 pagesQT Notes 7 PDFHidayathulla KhanNo ratings yet
- Complex Numbers and Quadratic EquationsDocument25 pagesComplex Numbers and Quadratic EquationsRohith ChakkingalNo ratings yet
- Scholarship Test Report 14th AUGUST 2022Document10 pagesScholarship Test Report 14th AUGUST 2022Renu SengarNo ratings yet
- 2013 Emic TeamDocument11 pages2013 Emic TeamLalangNo ratings yet