Professional Documents
Culture Documents
Free Ion Term Explanation
Uploaded by
skhjghwudosndgkCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Free Ion Term Explanation
Uploaded by
skhjghwudosndgkCopyright:
Available Formats
Free-Ion Terms to Ligand-field Terms
! Orbital term symbols for free atoms and ions are identical to symbols
for irreducible representations in R3.
" The irreducible representations of R3 include all possible
degeneracies.
L
There are no inherent symmetry restrictions on possible
orbital degeneracies in R3.
! In octahedral and tetrahedral crystal fields (Oh and Td) the highest
dimension irreducible representations are three-fold degenerate.
L
For Oh and Td complexes, free-ion terms with orbital degeneracies
greater than three (D, F, G, ...) must split into new terms, each of
which can have no higher than three-fold degeneracy.
" In crystal fields of lesser symmetry (e.g., D4h, D3) free-ion orbital
multiplicity terms with (2L + 1) > 2 must split as a result of the
descent in symmetry from R3 to the finite point group of the complex.
L
Ligand-field terms can have no higher orbital degeneracy than
allowed by the highest dimension irreducible representation of
the complex's point group.
" In any crystal field all the term symbols, including those that are not
split, are redefined and newly designated with the appropriate
Mulliken symbols of their corresponding irreducible representations
in the point group of the complex.
Why Terms Split in a Ligand-field
! Lifting the degeneracy among the d orbitals can destroy the
equivalences among microstates that give rise to a particular free-ion
term.
" Orbital assignments that were energetically equivalent in the free ion
may now be quite distinct in the environment of the complex.
These differences result in new collections of equivalent
microstates, each of which gives rise to a distinct ligand-field term.
The total number of microstates for the
configuration, as represented by Dt , remains the
same.
Example: Splitting of d 1 Terms in an Oh Field
! The 10 microstates for the free-ion configuration d 1 give rise to a 2D
term.
! In an octahedral field, the electron may have either the configuration t2g1
or eg1:
eg
eg
t2g
t2g
Ground State
Excited State
d 1 Oh Ground State Term
eg
t2g
Ground State
! In the ground state, the electron can be in any of the three t2g orbitals
with either spin orientation (ms = ).
" This makes six equivalent microstates.
" There are three equivalent orbital assignments, so the overall orbital
degeneracy (orbital multiplicity) is three.
(2L + 1) = 3
" There are only two overall spin orientations (Ms = ), so the spin
degeneracy (spin multiplicity) is two.
(2S + 1) = 2
The resulting term is 2T2g, in which the Mulliken symbol for
the orbital term is appropriately three-fold degenerate.
d 1 Oh Excited State Term
eg
t2g
Excited State
! In the excited state configuration eg1 the electron can be in either of the
two eg orbitals with either spin orientation (ms = ).
" This makes four equivalent microstates.
" There are two equivalent orbital assignments, so the overall orbital
degeneracy (orbital multiplicity) is two.
(2L + 1) = 2
" There are only two overall spin orientations (Ms = ), so the spin
degeneracy (spin multiplicity) is two.
(2S + 1) = 2
The associated term is 2Eg, in which the Mulliken symbol
for the orbital term is two-fold degenerate.
Total Degeneracy, Dt, Remains Unchanged
! Note that the total degeneracy of each ligand-field term, equivalent to
the number of microstates giving rise to it, is the product of its spin
degeneracy times its orbital degeneracy.
Dt (term) = (2L + 1)(2S + 1)
" For 2T2g we have
Dt (2T2g) = (2)(3) = 6
" For 2Eg we have
Dt (Eg) = (2)(2) = 4
The sum of total degeneracies of the ligand-field terms is
equivalent to Dt for the free-ion configuration d 1.
Dt (d 1) = Dt (2T2g) + Dt (2Eg) = 6 + 4 = 10
Determining Ligand-Field Terms from Free-ion Terms
! The fate of any free-ion term in the point group of a complex can be
determined by applying equations by which the characters for an
irreducible representation in R3 can be calculated:
P(E) = 2j + 1
P(i) = (2j + 1)
P(F) = sin(j +1/2)B
Making Free-ion Terms the Basis for a Representation
! It is possible to apply these equations to both the spin and orbital terms
(S and L states), but the field does not interact directly on the electron
spin in a chemical environment such as a complex ion.
" The new ligand-field terms will retain the original spin multiplicities
of the free-ion terms from which they originate.
" We only apply these equations to the L state of a free-ion term to
determine the identities of the terms that result from splitting in the
ligand field.
! In the last three equations with variable sign (), the positive sign is
used with gerade functions and the negative sign is used with ungerade
functions.
L
We will be concerned solely with terms arising from
configurations of d electrons, which are inherently gerade.
Therefore we will choose the positive expression in all
cases.
" Nonetheless, in noncentrosymmetric point groups (e.g., Td, D3h) the
resulting Mulliken symbol for the new state will not have a g
subscript notation, which would be inappropriate in such groups.
{If terms arising from p or f configurations are to be considered, use the
negative sign equations, because states arising from these are inherently
ungerade.}
Splitting of dn Free-ion Terms S, P, D, and F in Oh
! S state, for which L = 0, is nondegenerate.
" As with an s orbital, it has no angular dependence and no orientation
in space.
" Without using the equations, we conclude that in any point group an
S term will not be split and will bear the Mulliken symbol for the
totally symmetric representation.
L In Oh, S 6 A1g
Splitting of dn Free-ion Terms S, P, D, and F in Oh
! P state, for which L = 1, is triply degenerate.
" Substituting L = 1 into the equations for the operations of Oh gives
the following representation.
Oh
'P
8C3 6C2 6C4 3C2
0
-1
-1
i
3
6S4 8S6 3Fh 6Fd
1
-1
-1
" Inspection of the character table shows that 'P / T1g.
L In Oh, P 6 T1g
" A P term is not split, but becomes a triply degenerate T1g term.
{Recall that the three-fold degenerate p orbitals transform as T1u in Oh, but
as we now see a P state transforms as T1g. The transformations are
different because the p orbitals are inherently ungerade, but the P state
arising from a d configuration is inherently gerade.}
Splitting of dn Free-ion Terms S, P, D, and F in Oh
! D state, for which L = 2, is five-fold degenerate.
" Substituting L = 2 into the equations for the operations of Oh gives
the following representation.
Oh
'D
8C3 6C2 6C4 3C2
-1
-1
6S4 8S6 3Fh 6Fd
-1
-1
" This is identical to the reducible representation we obtained for d
orbitals.
L In Oh, D 6 Eg + T2g
" The five-fold degeneracy of the D free-ion term is lifted to become a
doubly degenerate term and a triply degenerate term because of the
restrictions on maximum degeneracy in Oh.
Splitting of dn Free-ion Terms S, P, D, and F in Oh
! F state, for which L = 3, is seven-fold degenerate.
" Substituting L = 3 into the equations for the operations of Oh gives
the following representation.
Oh
'F
8C3 6C2 6C4 3C2
1
-1
-1
-1
6S4 8S6 3Fh 6Fd
-1
" This reduces as 'F = A2g + T1g + T2g.
L In Oh, F 6 A2g + T1g + T2g
-1
-1
Splitting of Higher Terms
! The splitting of other states (G, H, I, etc.) can be determined in similar
manner, giving the following results:
Free-ion
Term
Terms in Oh
A1g
T1g
Eg + T2g
A2g + T1g + T2g
A1g + Eg + T1g + T2g
Eg + 2T1g + T2g
A1g + A2g + Eg + T1g + 2T2g
Example: Splitting of d 2 Free-Ion Terms in Oh
! The free-ion terms for the configuration nd2, in order of increasing
energy are
3
F < 1D < 3P < 1G < 1S
" Each of these terms will split into the ligand filed terms we have just
identified.
Free-ion terms
Octahedral terms
A2g 1Eg
T1g
T2g
Microstates
21
T1g 1A1g 1A1g
T2g
Eg
T1g
T2g
Dt = 21 + 5 + 9 + 9 + 1 = 45
Ligand-Field Terms in Other Fields
! The splittings of free-ion terms and the Mulliken symbols for the
ligand-field terms in other point groups can be obtained in similar
manner by making them bases for representations in the appropriate
point group.
" It is usually more efficient to use the correlation tables
" For example, inspection of the correlation table for Oh and Td shows
that the splittings are identical in both groups, except for the
omission of the subscript g for the tetrahedral states.
" Correlations with other groups (e.g., D4h, D3, D2d) are not as trivial,
but are equally straightforward.
Correlation Diagrams for Ligand Field Splitting
What is the energy order of the ligand field terms?
How will the energies of the terms change with changing )o?
! Group theory alone, cannot provide quantitative answers.
! It is possible to address the problem at least qualitatively with a
correlation diagram, which shows how the energies of terms change as
a function of the ligand field strength, measured as )o.
! To construct the correlation diagram, we look at two extremes:
" Left side: A weak field, just strong enough to lift the R3 free-ion term
degeneracies.
On the left side of the diagram we show the energies of the free-ion
terms and the Mulliken symbols for the terms into which they are
split in a weak octahedral field.
" Right side: A hypothetical extremely strong field.
At the limit of an extremely large )o separation between t2g and eg
orbitals, we assume that interactions between electrons in separate
orbitals are negligible.
At this limit we can assess the energy order of the possible
electronic configurations for the ground state and all excited states.
We can then identify the terms that will emerge from each of these
configurations in a slightly less strong field, where electronic
interactions begin to be felt.
Layout of a Term Splitting Correlation Diagram
Free-Ion terms
listed here
Weak-Field terms
listed here
Strong-Field terms
listed here
t2g ee g f
t2g ce g d
t2g a e g b
Correlation lines
linking Weak-Field to
Strong-Field terms
Free Ion Weak Field
o
Strong Field
Extreme-Field electronic
configurations in energy order
Extreme Field
Constructing A Correlation Diagram for d 2
The job of constructing the diagram amounts to
determining the correlations between terms in the weak
field and the terms in the strong field.
! General Approach - The Method of Descending Symmetry
(Bethe).
" Rigorous, generally applicable, but tedious.
! The Noncrossing Rule is observed: Correlation lines for
states of the same symmetry and same multiplicity do not
cross, but rather repel one another, thereby increasing their
relative energy separation beyond a certain minimum as field
strength increases.
You might also like
- 122266296133461Document14 pages122266296133461Jaydeep DeoreNo ratings yet
- The electronic spectra of transition metal complexesDocument22 pagesThe electronic spectra of transition metal complexesVishnu ChariNo ratings yet
- Understanding Atomic Term SymbolsDocument13 pagesUnderstanding Atomic Term SymbolsAnish RaoNo ratings yet
- Lecture 10Document7 pagesLecture 10Debopam RayNo ratings yet
- Electronic Spectra of ComplexesDocument82 pagesElectronic Spectra of Complexesirembasar2000No ratings yet
- CH2422 Electronic Spectra of Transition MetalsDocument6 pagesCH2422 Electronic Spectra of Transition MetalsJohnNo ratings yet
- Electronic Spectra of TM ComplexesDocument35 pagesElectronic Spectra of TM Complexesbits_who_am_iNo ratings yet
- Electronic Spectra of Transition MetalDocument39 pagesElectronic Spectra of Transition MetaljohnwilliamsNo ratings yet
- Transition Metal Complexes d1 d9 StatesDocument40 pagesTransition Metal Complexes d1 d9 StatesadelNo ratings yet
- 2 ElectronicDocument23 pages2 ElectronicHandugan Quinlog NoelNo ratings yet
- Electronic Spectra Reveal Ligand Field SplittingDocument23 pagesElectronic Spectra Reveal Ligand Field SplittingHandugan Quinlog NoelNo ratings yet
- Diagram Tanabe PoncoDocument10 pagesDiagram Tanabe PoncounsaniaNo ratings yet
- Visible spectra metal complexesDocument29 pagesVisible spectra metal complexesNoriko MedorumaNo ratings yet
- Eldas AnorDocument8 pagesEldas AnorHaryadi Nugraha PutraNo ratings yet
- SPECTRAL CALCULATION OF ORGEL AND TANABE-SUGANO DIAGRAMSDocument18 pagesSPECTRAL CALCULATION OF ORGEL AND TANABE-SUGANO DIAGRAMSTiwari VishalNo ratings yet
- Bonding ProblemDocument219 pagesBonding ProblemIndresh YadavNo ratings yet
- Tanabe-Sugano Diagram ExplainedDocument5 pagesTanabe-Sugano Diagram Explainedd4nk4rNo ratings yet
- Ko Ordination S ChemieDocument31 pagesKo Ordination S ChemiePaoBenítezNo ratings yet
- Atomic Term SymbolsDocument4 pagesAtomic Term SymbolsM IkhsanNo ratings yet
- Group Theory-Part 12 Correlation DiagramsDocument36 pagesGroup Theory-Part 12 Correlation Diagramsnancyboy100% (1)
- Unit 5 Coordination Chemistry: Graduate Center Inorganic Chemistry (Fall 2012)Document39 pagesUnit 5 Coordination Chemistry: Graduate Center Inorganic Chemistry (Fall 2012)Carlos Cesar Lopez SuarezNo ratings yet
- Inorganic Spectoscopy-UV-VisDocument100 pagesInorganic Spectoscopy-UV-VisUsama El-Ayaan100% (5)
- CH437Electronic Spectroscopy 1Document25 pagesCH437Electronic Spectroscopy 1Edukondalu NamepalliNo ratings yet
- 5.04 Principles of Inorganic Chemistry Ii : Mit OpencoursewareDocument9 pages5.04 Principles of Inorganic Chemistry Ii : Mit OpencoursewareIsrael PobleteNo ratings yet
- Coordination Chemistry Bonding in Transition-Metal ComplexesDocument45 pagesCoordination Chemistry Bonding in Transition-Metal ComplexessandraagustinNo ratings yet
- Ligand Field N MOTDocument12 pagesLigand Field N MOTLata Sharma100% (1)
- Zero Field SplittingDocument3 pagesZero Field SplittingHenrique CastroNo ratings yet
- MIT OCW Principles of Inorganic Chemistry II Lecture on Octahedral ML6 Sigma ComplexesDocument7 pagesMIT OCW Principles of Inorganic Chemistry II Lecture on Octahedral ML6 Sigma Complexessanskarid94No ratings yet
- Term Symbols and Selection Rules in Atomic SpectroscopyDocument4 pagesTerm Symbols and Selection Rules in Atomic SpectroscopyIqbal Aljabir PujionoNo ratings yet
- Answers To Assignment2-2009Document6 pagesAnswers To Assignment2-2009ElmIeyHakiemiEyNo ratings yet
- Electronic SoectraDocument25 pagesElectronic SoectraAbhinav KumarNo ratings yet
- Class 4Document13 pagesClass 4Muskan BiswalNo ratings yet
- Electronic SpectrosDocument22 pagesElectronic SpectrosBandita DattaNo ratings yet
- Chapter 7 Transition Metal ComplexesDocument48 pagesChapter 7 Transition Metal ComplexesrabiaNo ratings yet
- Lecture 6Document7 pagesLecture 6ankara271828No ratings yet
- Introduction To Crystal Field TheoryDocument11 pagesIntroduction To Crystal Field TheoryMa'arif A. Syafii100% (1)
- Teoria Do Campo Ligante - Part IIDocument25 pagesTeoria Do Campo Ligante - Part IIArthurGrafdeSousaNo ratings yet
- Lecture-11: Study Material Chem-524Document10 pagesLecture-11: Study Material Chem-524Abdul Munaf Ali NasirNo ratings yet
- Electronic Spectroscopy of Transition Metal CompoundsDocument24 pagesElectronic Spectroscopy of Transition Metal CompoundsBruno Ramos de LimaNo ratings yet
- d-orbital splitting in Td vs Oh complexesDocument13 pagesd-orbital splitting in Td vs Oh complexesJK JKNo ratings yet
- ChemDocument7 pagesChem22PCH103 PRAKASH RNo ratings yet
- Term Symbols & Spitting of Terms - Transition Metal ComplexesDocument16 pagesTerm Symbols & Spitting of Terms - Transition Metal Complexesramukaka100% (3)
- Coordination Chemistry III 2ndDocument34 pagesCoordination Chemistry III 2ndharis100% (2)
- Spectroscopic Analysis of Transition Metal ComplexesDocument10 pagesSpectroscopic Analysis of Transition Metal ComplexesJohn Kenneth Ala SanguezaNo ratings yet
- Transition Metal ReviewDocument12 pagesTransition Metal ReviewShyama ShaliniNo ratings yet
- Atomic Term Symbols ExplainedDocument20 pagesAtomic Term Symbols ExplainedRirin Zarlina100% (1)
- Molecular Term SymbolsDocument5 pagesMolecular Term Symbols1jerushaNo ratings yet
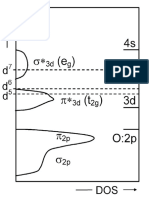
- Monoelectronic Band Structure For A Cubic PerovskiteDocument1 pageMonoelectronic Band Structure For A Cubic PerovskiteSJNo ratings yet
- Radial Wave Function and Angular Wave FunctionsDocument8 pagesRadial Wave Function and Angular Wave FunctionsBhavesh Garg100% (1)
- CH 14. Electronic Spectros PDFDocument9 pagesCH 14. Electronic Spectros PDFiq3pevicNo ratings yet
- J Values ExplndDocument20 pagesJ Values ExplndAri SinghNo ratings yet
- Coordination Chemistry Crystal Field Theory (CFTDocument15 pagesCoordination Chemistry Crystal Field Theory (CFTveronicaNo ratings yet
- Handout For Russell-Saunders Coupling PDFDocument12 pagesHandout For Russell-Saunders Coupling PDFAditiNo ratings yet
- Sol4 99Document9 pagesSol4 99HossainNo ratings yet
- Solutions The: So Are ToDocument1 pageSolutions The: So Are ToKamleshkekane1No ratings yet
- Tables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiFrom EverandTables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiNo ratings yet
- Internal Conversion Coefficients for Multipolarities E1,…, E4, M1,…, M4From EverandInternal Conversion Coefficients for Multipolarities E1,…, E4, M1,…, M4Katharine WayNo ratings yet
- Simple Algebras, Base Change, and the Advanced Theory of the Trace Formula. (AM-120), Volume 120From EverandSimple Algebras, Base Change, and the Advanced Theory of the Trace Formula. (AM-120), Volume 120No ratings yet
- Discrete Series of GLn Over a Finite Field. (AM-81), Volume 81From EverandDiscrete Series of GLn Over a Finite Field. (AM-81), Volume 81No ratings yet
- Thermodynamic analysis of phase transitions in a substanceDocument6 pagesThermodynamic analysis of phase transitions in a substanceskhjghwudosndgkNo ratings yet
- Chem 212 Homework 1 KeyDocument7 pagesChem 212 Homework 1 KeyskhjghwudosndgkNo ratings yet
- Solution 21Document1 pageSolution 21skhjghwudosndgkNo ratings yet
- Solution 18Document2 pagesSolution 18skhjghwudosndgkNo ratings yet
- Solution 20Document5 pagesSolution 20skhjghwudosndgkNo ratings yet
- Solution 22Document1 pageSolution 22skhjghwudosndgkNo ratings yet
- Solution 23Document9 pagesSolution 23skhjghwudosndgkNo ratings yet
- Solution 19Document5 pagesSolution 19skhjghwudosndgkNo ratings yet
- Solution 14Document3 pagesSolution 14skhjghwudosndgkNo ratings yet
- Solution 16Document6 pagesSolution 16skhjghwudosndgkNo ratings yet
- Solution17 2Document2 pagesSolution17 2skhjghwudosndgkNo ratings yet
- Solution10 11Document8 pagesSolution10 11skhjghwudosndgkNo ratings yet
- Solution 13Document7 pagesSolution 13skhjghwudosndgkNo ratings yet
- Solution 15Document6 pagesSolution 15skhjghwudosndgkNo ratings yet
- Solution9 SkipDocument5 pagesSolution9 SkipskhjghwudosndgkNo ratings yet
- PP . - (L J D7 N ( J DP: - Dy (Yljdt - (PcpydpDocument6 pagesPP . - (L J D7 N ( J DP: - Dy (Yljdt - (PcpydpskhjghwudosndgkNo ratings yet
- Solution 3Document1 pageSolution 3skhjghwudosndgkNo ratings yet
- Solution 1Document2 pagesSolution 1skhjghwudosndgkNo ratings yet
- Solution 7Document4 pagesSolution 7skhjghwudosndgkNo ratings yet
- Solution 8Document3 pagesSolution 8skhjghwudosndgkNo ratings yet
- Trash Trash Fishing TrashDocument1 pageTrash Trash Fishing TrashskhjghwudosndgkNo ratings yet
- Solution 5Document4 pagesSolution 5skhjghwudosndgkNo ratings yet
- Solution 4Document3 pagesSolution 4skhjghwudosndgkNo ratings yet
- Solution 6Document3 pagesSolution 6skhjghwudosndgkNo ratings yet
- Solution 2Document2 pagesSolution 2skhjghwudosndgkNo ratings yet
- Ex Ophtalmo Eng 1Document4 pagesEx Ophtalmo Eng 1Roxana PascalNo ratings yet
- Natural Law Theory ApproachDocument35 pagesNatural Law Theory ApproachseventhwitchNo ratings yet
- Makalah Bahasa Inggris - Narrative TextDocument21 pagesMakalah Bahasa Inggris - Narrative TextFenny KartikaNo ratings yet
- Mathematics: Minimum Level Learning MaterialDocument60 pagesMathematics: Minimum Level Learning MaterialTusar SardarNo ratings yet
- Approach To Malabsorption (SANJAY)Document58 pagesApproach To Malabsorption (SANJAY)Sanjay KumarNo ratings yet
- Why Check Valves SlamDocument2 pagesWhy Check Valves SlamBramJanssen76No ratings yet
- Site Master FileDocument51 pagesSite Master FileMilonhg100% (2)
- BiodiversityDocument9 pagesBiodiversityVienica Dauz Mico Balbin100% (1)
- Data Biostataplus Sbi2014-EDocument4 pagesData Biostataplus Sbi2014-ELucila Milagros PinillosNo ratings yet
- Mill Test Certificate: Jindal Stainless (Hisar) LimitedDocument1 pageMill Test Certificate: Jindal Stainless (Hisar) Limitedhemantmech09920050% (2)
- Hydraulic Power Steering System Design PDFDocument16 pagesHydraulic Power Steering System Design PDFAdrianBirsan100% (1)
- Inakyd 3623-X-70Document2 pagesInakyd 3623-X-70roybombomNo ratings yet
- Total Tattoo-June 2021Document114 pagesTotal Tattoo-June 2021Comicgek100% (2)
- Consumer preference towards branded milk: A comparative analysis of Verka milk and Amul milkDocument12 pagesConsumer preference towards branded milk: A comparative analysis of Verka milk and Amul milkBhawna RehanNo ratings yet
- Dental Radiographs and Photographs in Human Forensic IdentificationDocument8 pagesDental Radiographs and Photographs in Human Forensic IdentificationBudi PurnomoNo ratings yet
- The Blue Hotel PDFDocument22 pagesThe Blue Hotel PDFGabriel OvidorNo ratings yet
- 1 s2.0 S2210803316300781 MainDocument8 pages1 s2.0 S2210803316300781 MainGilang Aji P. EmonNo ratings yet
- Oil Safety Data SheetDocument19 pagesOil Safety Data Sheetemailsepamku gorgomNo ratings yet
- CERT Basic Training Participant Manual - 2011Document332 pagesCERT Basic Training Participant Manual - 2011jegodfreyNo ratings yet
- Plant LayoutDocument16 pagesPlant LayoutAli MahmoudNo ratings yet
- List of Computer Networking DevicesDocument1 pageList of Computer Networking Deviceskamit17102900100% (1)
- Pump Characteristics ExperimentDocument7 pagesPump Characteristics ExperimentJam JoNo ratings yet
- The LM393Document2 pagesThe LM393mayron vasquezNo ratings yet
- Fodor Hungary Between East and WestDocument22 pagesFodor Hungary Between East and WestFatih YucelNo ratings yet
- JMJ Marist Brothers Notre Dame of Marbel University Integrated Basic Education Department City of Koronadal, South CotabatoDocument13 pagesJMJ Marist Brothers Notre Dame of Marbel University Integrated Basic Education Department City of Koronadal, South CotabatoNestor Gerotape DiosanaNo ratings yet
- SAFETY AND LOSS PREVENTION FOR CHEMICAL PROCESS FACILITIESDocument13 pagesSAFETY AND LOSS PREVENTION FOR CHEMICAL PROCESS FACILITIESKinosraj KumaranNo ratings yet
- Comparison Study of Conventional Hot-Water and Microwave Blanching at Different Timetemperaturepower Combinations On The Quality of Potatoes.Document72 pagesComparison Study of Conventional Hot-Water and Microwave Blanching at Different Timetemperaturepower Combinations On The Quality of Potatoes.DavldSmith100% (1)
- PCS PADDLE SHIFTER INSTALL GUIDEDocument21 pagesPCS PADDLE SHIFTER INSTALL GUIDEAndreas T P ManurungNo ratings yet
- Tiger 690 Conversion PDFDocument8 pagesTiger 690 Conversion PDFGerardo Esteban Lagos RojasNo ratings yet
- Fundamentals of VolleyballDocument2 pagesFundamentals of VolleyballLawrence CezarNo ratings yet