Math 1040

Tiffany Hilton
October 1, 2018
Skittles Project part 3

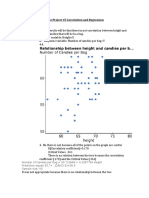
“Can height be used to predict the number of candies that will be in a bag of Skittles you
purchase?”
1. I do not believe that the height of each class mate can predict the total number of
candies in each individual’s skittles bag because there is no logical way to be able to
predict the number of candies in the bag you purchased based on your height.
2. The explanatory variable (x) would be the height of the person buying the skittles bag and
the response variable (y) would be the number of candies per bag
3. Simple linear regression results:
Dependent Variable: Total
Independent Variable: Height
Total = 64.32367 - 0.066960037 Height
Sample size: 35
R (correlation coefficient) = -0.12087521
R-sq = 0.014610816
Estimate of error standard deviation: 2.3176362
Parameter estimates:
Parameter Estimate Std. Err. Alternative DF T-Stat P-value
Intercept 64.32367 6.2749803 ≠ 0 33 10.250816 <0.0001
Slope -0.066960037 0.095724999 ≠ 0 33 -0.69950418 0.4891

Analysis of variance table for regression model:

Source DF SS MS F-stat P-value
Model 1 2.6282771 2.6282771 0.4893061 0.4891
Error 33 177.25744 5.3714375
Total 34 179.88571
4. No, there is no relationship between the height of each class mate and the number of
candies in the bag they purchased because the absolute value of the correlation
coefficient (-0.12087521) is smaller than the critical value (0.361). This is what I predicted
because there is no way to be able to predict the number of candies in the bag you
purchased based on your height.
5. Regression equation: y^= -0.067x+64.32
Using the regression equation to calculate the number of skittles that would be expected
to be in the bag that was purchased by 63.5 inches tall would be:
y= -0.067(63.5)+64.32=60 skittles.
It not appropriate to use this equation to make a prediction because there is no
relationship between the two variables
6. R2 is the coefficient of determination. To use the liner regression and to interpret R2
there must be a liner relationship between X and Y, and there is not. The closer the Ys are
 to the regression line the stronger correlation. In this case R2=0.014610816 which
means that 1.5% of the variation in the response variable is explained by the least square
regression line.
7. No, it would not be appropriate to predict the number of candies in a bag purchased by
Yao Ming because his height is out of the scope of the model.
8. Data values

-X-height
69,64,63,74,67,60,70
-Y-# of skittles
56,59,60,60,61,62,62

Correlation Coefficient= -0.219

-Regression equation: y^=-0.096x+66.4
-Critical value=0.754
-There is no significant relationship because the absolute value of the correlation
coefficient is smaller than the critical value