Notas de Clculo III

Curso obligatorio para las

Licenciaturas en:
Actuara
Matemticas
Enseanza de las Matemticas
Universidad Autnoma de Yucatn
Dr. Jos Matas Navarro Soza
1
INTRODUCCIN
Este curso trata de generalizar algunos de los conceptos y tcnicas del clculo
de una variable para funciones de varias variables, un esfuerzo que comenz en
el curso de Clculo II. Para lograr una comprensin de los conceptos, al mismo
tiempo que se obtienen las habilidades para calcular derivadas e integrales en
varias variables, resulta de mucha utilidad observar las similitudes y
diferencias con los conceptos y tcnicas correspondientes en una variable. Con
el objetivo de suavizar el camino, primero se desarrollan los temas en
dimensiones bajas, para despus generalizar a cualquier nmero de
dimensiones. Se muestran ejemplos y aplicaciones en el plano y el espacio
tridimensional que ayuden a desarrollar tanto la intuicin geomtrica como las
habilidades para determinar los clculos necesarios en la solucin de un
problema especco. Tambin se enuncian algunos teoremas importantes,
dando las pruebas de aquellos teoremas que resultan accesibles en este nivel,
que pueden servir para lograr una evolucin paulatina de la madurez
matemtica del estudiante y que forman parte de los conocimientos necesarios
para desarrollar temas ms avanzados de clculo y sus aplicaciones.
2
CONTENIDO
1. Derivacin.
1.1. Curvas.
1.1.1. Curvas parametrizadas.
1.1.2. Derivada y vector tangente.
1.1.3. Propiedades de la derivada.
1.2. Campos escalares.
1.2.1. Curvas y supercies de nivel.
1.2.2. Conjuntos abiertos y cerrados.
1.2.3. Derivadas parciales.
1.2.4. Ejemplos en dos y tres dimensiones.
1.2.5. Gradiente.
1.2.6. Diferenciabilidad.
1.2.7. Regla de la Cadena.
1.2.8. Planos tangentes a supercies de nivel.
1.2.9. Planos tangentes a grcas de funciones.
1.2.10. Derivadas direccionales.
1.2.11. Derivadas de orden superior.
1.2.12. Mximos y mnimos de funciones de dos variables.
1.3. Campos Vectoriales.
1.3.1. La derivada de un campo vectorial.
1.3.2. La matriz Jacobiana.
1.3.3. Ejemplos en dimensiones 1, 2 y 3.
1.3.4. Regla de la Cadena.
1.3.5. Ejemplos en dimensiones 1, 2 y 3.
1.3.6. Funciones inversas y funciones implcitas.
1.3.7. Ejemplos en dimensiones 1, 2 y 3.
1.3.8. Divergencia y Rotacional.
1.4. Ejercicios y problemas.
2. Integracin en dos y tres variables.
2.1. Integral de Riemann.
2.1.1. Deniciones bsicas.
3
2.2. Existencia de la integral.
2.2.1. Integrabilidad.
2.2.2. Medida cero y contenido cero.
2.2.3. Criterio de integrabilidad para funciones discontinuas.
2.3. Propiedades bsicas de la integral.
2.3.1. Linealidad y aditividad.
2.3.2. Teorema del Valor Medio.
2.4. El Teorema de Fubini.
2.5. Integrales dobles y triples.
2.5.1. Integrales dobles sobre regiones elementales.
2.5.2. Cambio del orden de integracin.
2.5.3. Integrales triples.
2.5.4. Teorema del cambio de variables.
2.6. Ejercicios y problemas.
3. Integrales sobre Curvas y Supercies.
3.1. Integrales de lnea.
3.1.1. Integral de lnea de campos escalares.
3.1.2. Integral de lnea de campos vectoriales.
3.1.3. Teorema de Green.
3.2. Integrales de supercie.
3.2.1. Supercies parametrizadas y orientadas.
3.2.2. Integrales de supercie.
3.3. Ejercicios y problemas.
4
1: Derivacin
1.1. Curvas.
1.1.1. Curvas parametrizadas.
Sea 1 un intervalo abierto de nmeros reales. Una curva parametrizada en
R
n
es una funcin que a cada nmero real t en 1 le asocia un vector de R
n
. Si
c denota una curva denida en 1, usamos c(t) para denotar el vector asociado
a t por la funcin c : 1 R
n
y se escribe la regla de correspondencia como
c(t) = (r
1
(t) , . . . , r
n
(t)) ,
donde cada r
I
(t) es una funcin de una variable del clculo elemental.
1.1.2. Derivada y vector tangente.
Se dice que esta curva es diferenciable en t = t
1
si cada una de las funciones
componentes r
I
: 1 R es diferenciable en t = t
1
. Si la curva es diferenciable
denimos su derivada por
dc
dt
=
_
dr
1
dt
, . . . ,
dr
n
dt
_
,
la cual tambin se denota por c
0
(t). Ver las referencias [1] y [2].
Ejemplo. La curva c : R R
3
denida por
c(t) = (cos t, :c: t, t)
le asigna a cada nmero real t el vector (cos t, :c: t, t), el cual se puede
identicar con el punto del espacio tridimensional que describe una hlice, pues
como r
2
1
(t) +r
2
2
(t) = 1 para todo valor de t, resulta que la proyeccin del punto
(cos t, :c: t, t) sobre el plano rj es una circunferencia de radio 1 y como
. (t) = t, la altura crece conforme t aumenta. La derivada para cada t R es
c
0
(t) = (:c: t, cos t, 1) .
A la derivada de una curva tambin se le denomina vector tangente o vector
velocidad, dependiendo si se quiere ver con los ojos del gemetra o con los del
fsico. En cualquier caso representa la razn de cambio de la funcin c(t).
La lnea tangente a una curva c en un punto correspondiente a t = t
1
se
dene como la lnea recta que pasa por el punto c(t
1
) en la direccin del
5
vector c
0
(t
1
), si se cumple que c
0
(t
1
) ,= 0. En los puntos de la curva donde la
derivada se anula, la lnea tangente no existe.
Ejemplo. Encontrar ecuaciones paramtricas para la lnea tangente a la
curva c : R R
2
denida por c(t) = (:c: t, cos t) en t = ,3.
La derivada es c
0
(t) = (cos t, :c: t). Por lo tanto la direccin es el vector
c
0
(,3) = (
1
2
,
_
3
2
).
Como c(,3) = (
p
3
2
,
1
2
) es el punto de la curva por donde pasa esta lnea
tangente, su ecuacin es
r(t) = c(,3) +t c
0
(,3),
=
_
_
3
2
,
1
2
_
+t
_
1
2
,
_
3
2
_
,
=
_
_
3
2
+
1
2
t,
1
2

_
3
2
t
_
,
de ah que las ecuaciones paramtricas buscadas son:
r(t) =
_
3
2
+
1
2
t, j(t) =
1
2

_
3
2
t.
1.1.3. Propiedades de la derivada.
Como la derivada de una curva se dene por las derivadas de sus funciones
componentes, las reglas de la derivacin resultan ser similares a las del clculo
ordinario en una variable.
Reglas de derivacin de curvas. Sean c, c
1
y c
2
curvas diferenciables
denidas en el mismo intervalo 1 de nmeros reales y )(t) una funcin
diferenciable real denida en 1. Entonces la suma c
1
(t) +c
2
(t) y los
productos )(t)c
1
(t), c
1
(t) c
2
(t) son diferenciables en 1 y se cumplen las
siguientes reglas:
d
dt
(c
1
(t) +c
2
(t)) =
dc
1
(t)
dt
+
dc
2
(t)
dt
,
d
dt
()(t)c(t)) = )(t)
dc(t)
dt
+
d)(t)
dt
c(t),
d
dt
(c
1
(t) c
2
(t)) = c
1
(t)
dc
2
(t)
dt
+
dc
1
(t)
dt
c
2
(t).
6
Las demostraciones de todas las reglas de derivacin anteriores son similares y
se basan en las correspondientes propiedades de la derivacin de funciones de
una variable. Por ejemplo, para la segunda regla procedemos como sigue. Sean
)(t) una funcin real valuada diferenciable y
c(t) = (r
1
(t) , . . . , r
n
(t))
una curva diferenciable, ambas denidas en un intervalo 1 de nmeros reales.
Entonces por denicin,
)(t)c(t) = ()(t)r
1
(t), . . . , )(t)r
n
(t)) .
Derivando cada componente con respecto a t y aplicando la regla de la
derivada de un producto de funciones de una variable, resulta que
d
dt
()(t)c(t)) =
_
)(t)
dr
1
(t)
dt
+
d)(t)
dt
r
1
(t), . . . , )(t)
dr
n
(t)
dt
+
d)(t)
dt
r
n
(t)
_
.
Usando ahora la regla de la suma de dos vectores, podemos expresar el lado
derecho como
_
)(t)
dr
1
(t)
dt
, . . . , )(t)
dr
n
(t)
dt
_
+
_
d)(t)
dt
r
1
(t), . . . ,
d)(t)
dt
r
n
(t)
_
,
lo cual es
)(t)
_
dr
1
(t)
dt
, . . . ,
dr
n
(t)
dt
_
+
d)(t)
dt
(r
1
(t), . . . , r
n
(t)),
o bien,
)(t)
dc(t)
dt
+
d)(t)
dt
c(t).
Si )(t) = c, una constante, entonces claramente se tiene que
d
dt
(c c(t)) = c
dc(t)
dt
.
1.2. Campos escalares
1.2.1. Curvas y supercies de nivel.
Se dene un campo escalar como una funcin de varias variables ) : R
n
R,
denida por alguna regla de correspondencia que a cada punto (r
1
, . . . , r
n
) del
:-espacio Euclidiano le asocia un nmero real )(r
1
, . . . , r
n
). El conjunto de
nivel c de ) se dene por la imagen inversa de c, esto es,
)
1
(c) = (r
1
, . . . , r
n
) R
n
[ ) (r
1
, . . . , r
n
) = c .
7
Para funciones de dos variables, los conjuntos de nivel son curvas en R
2
denidas por ecuaciones del tipo
)(r
1
, r
2
) = c,
mientras que para funciones de tres variables los conjuntos de nivel son
supercies en R
3
denidas por ecuaciones de la forma
)(r
1
, r
2
, r
3
) = c.
Ver las referencias [1], [2] y [3].
Ejemplo. Las curvas de nivel de la funcin )(r, j) = r
2
+j
2
son
circunferencias para c 0, un punto (el origen) para c = 0 y no existen para
c < 0.
Ejemplo. Las supercies de nivel para )(r, j, .) = r
2
+j
2
.
2
son
hiperboloides para todo valor de c.
Ahora comenzaremos a estudiar la diferenciabilidad de funciones de varias
variables. Para denir la derivada de una funcin ) (r
1
, . . . , r
n
) necesitamos el
concepto de subconjunto abierto de R
n
, el cual generaliza la idea de "cercana"
en dimensiones superiores.
1.2.2. Conjuntos abiertos y cerrados.
Denicin. Sea j un punto de R
n
y - 0. La bola abierta de radio - y
centro j es el subconjunto de R
n
denido por
1
:
(j) = R
n
[ |j | < - .
Ver las referencias [1] y [2].
Se puede imaginar a 1
:
(j) como el conjunto de todos los puntos de R
n
que
estn cercanos a j hasta una distancia menor que -. Si cambiamos la
desigualdad |j | < - en la denicin de bola abierta por |j | _ -,
obtenemos el concepto de bola cerrada. La esfera de radio - con centro en j es
el conjunto
o
n1
:
(j) = R
n
[ |j | = - ,
donde el superndice : 1 es una indicacin de la dimensin del conjunto, un
concepto de la topologa. Por ejemplo, la 2-esfera de radio 1 con centro en el
origen
o
2
:
(0) =
_
(r, j, .) R
3
[ r
2
+j
2
+.
2
= -
2
_
8
es bidimensional en el sentido que los puntos que la conforman viven en una
supercie. La nocin de conjunto abierto en R
n
generaliza la idea de que
todos los puntos sucientemente cercanos a cada uno de sus puntos tambin
pertenecen al conjunto abierto.
Denicin. Sea l un conjunto de puntos de R
n
. Se dice que l es abierto, si
para cada uno de sus puntos j l existe una bola abierta 1
:
(j) con centro en
j de algn radio - 0 contenida en l.
Denicin. Un conjunto de puntos de R
n
es cerrado si su complemento
R
n
es abierto.
Denicin. Un conjunto de puntos 1 de R
n
es acotado si para todo punto
j 1 existe un nmero a 0 tal que |j| _ a. En otras palabras: 1 es
acotado si existe una bola de radio a con centro en el origen que contiene al
conjunto 1.
Ver las referencias [1], [2], [3] y [6].
Ejemplo. En el plano R
2
, el primer cuadrante sin el eje r y sin el eje j es un
conjunto abierto. El eje r no es abierto como subconjunto de R
2
, pues dado
cualquier punto del eje r no se puede encontrar un disco abierto con centro en
dicho punto y que est contenido en el eje r. Similarmente, el intervalo de
nmeros reales
(1, 1) = r R [ 1 < r < 1
es abierto en R, pero no es abierto en R
2
.
Ejemplo. Sea l la bola abierta en R
n
de radio a 0 con centro en el origen.
Veamos que l es abierto en R
n
. Para demostrarlo, tomemos cualquier punto
j de esta bola. Tenemos que |j| < a por denicin. Ahora llamemos c a la
diferencia
c = a |j| .
Si es cualquier punto de R
n
tal que | j| < c, es decir, 1
c
(j), entonces
la desigualdad del tringulo y la ley transitiva implican lo siguiente:
|| _ | j| +|j| < a |j| +|j| = a,
es decir, pertenece a la bola de radio a con centro en el origen, l. Por lo
tanto 1
c
(j) l, probando con esto que l es un conjunto abierto de R
n
.
1.2.3. Derivadas parciales.
Para una funcin ) : l R
n
R, denida en un conjunto abierto l por una
regla de correspondencia que le asocia a un punto (r
1
, . . . , r
n
) l un nmero
9
) (r
1
, . . . , r
n
), podemos tomar / sucientemente pequeo para tener
(r
1
+/, r
2
, . . . , r
n
) contenido en l de manera que ) est denida en
(r
1
+/, r
2
, . . . , r
n
) y as tenga sentido formar el cociente
) (r
1
+/, r
2
, . . . , r
n
) ) (r
1
, r
2
, . . . , r
n
)
/
.
Si existe el lmite de este cociente cuando / 0, le llamaremos la derivada
parcial respecto a r
1
y la denotaremos por cualquiera de los siguientes
smbolos:
1
1
),
0)
0r
1
, )
r1
, 1
r1
),
como mejor convenga a la claridad dependiendo del contexto.
En general, para cualquier variable r
I
, se dene
0)
0r
I
= lim
|!0
) (r
1
, . . . , r
I
+/, . . . , r
n
) ) (r
1
, . . . , r
I
, . . . , r
n
)
/
,
de donde podemos obtener la siguiente interpretacin: una derivada parcial
respecto a una de las variables es una derivada ordinaria cuando se consideran
como constantes las otras variables. En el caso bidimensional, tenemos que
0)
0r
= lim
|!0
) (r +/, j) ) (r, j)
/
,
0)
0j
= lim
|!0
) (r, j +/) ) (r, j)
/
,
si existen estos lmites.
Ver [1], [3], [4] y [6].
Ejemplo. Sea )(r, j) = :c: rj. Entonces
0)
0j
(r, j) = (cos rj) r,
y de ah que, por ejemplo,
0)
0j
(1, ) = (cos ) 1 = 1.
Similarmente, es fcil ver que
0)
0j
_
3,

4
_
=
3
_
2
.
10
Por otro lado,
0)
0r
(r, j) = (cos rj) j,
y
0)
0r
(1, ) = (cos ) = .
1.2.5. Gradiente.
Para una funcin de : variables, ) (r
1
, . . . , r
n
), si existen todas las derivadas
parciales respecto a cada una de las variables r
1
, . . . , r
n
, podemos formar un
vector con todas ellas. El vector
_
0)
0r
1
,
0)
0r
2
, . . . ,
0)
0r
n
_
es llamado el gradiente de ) y se denota por grad), o tambin por \). Para
una funcin de dos variables,
\)(r, j) =
_
0)
0r
,
0)
0j
_
.
Ver [1] y [2].
Ejemplo. Sea )(r, j) = r
2
j
3
. Entonces
\)(r, j) =
_
2rj
3
, 3r
2
j
2
_
,
as, por ejemplo,
\) (1, 2) = (16, 12) .
El gradiente es un ejemplo de campo vectorial, pues le asocia un vector a cada
punto del dominio.
Usando las propiedades de la derivacin en una variable es fcil ver que se
tiene el siguiente teorema.
Teorema. Sean ) y q dos funciones denidas en un abierto l R
n
tales que
sus derivadas parciales respecto a todas las variables existen en cada punto de
l. Entonces
\() +q) = \) +\q,
11
y
\(c)) = c\)
para todo nmero real c.
1.2.6. Diferenciabilidad.
Se conocen funciones que son discontinuas en un punto a pesar de que s
existen todas sus derivadas parciales respecto a todas sus variables en ese
punto. Por ejemplo, para
)(r, j) =
_

_
0 :i (r, j) = (0, 0)
rj
r
2
+j
2
:i (r, j) ,= (0, 0)
se tiene que
0)
0r
(0, 0) = lim
|!0
1
/
) (/, 0) = lim
|!0
0
/
3
= lim
|!0
0 = 0,
y tambin existe
0)
0j
(0, 0) = lim
|!0
1
/
) (0, /) = lim
|!0
0
/
3
= lim
|!0
0 = 0,
sin embargo, si elegimos aproximarnos al origen a travs de las trayectorias
j = r, r = 0,
resultan lmites diferentes:
lim
r!0
=r
)(r, j) = lim
r!0
r
2
2r
2
= lim
r!0
1
2
=
1
2
,
lim
r!0
r=0
)(r, j) = lim
r!0
0
j
2
= lim
r!0
0 = 0,
por lo tanto no existe el lmite de ) (r, j) cuando (r, j) (0, 0). En
consecuencia, esta funcin es discontinua en el origen, a pesar de que existen
sus derivadas parciales en el origen. De ah que sea necesario un concepto ms
fuerte de "diferenciabilidad" que la mera existencia de las derivadas parciales,
si queremos que la diferenciabilidad implique la continuidad. Las siguientes
consideraciones van encaminadas hacia esa meta. Sea ) una funcin denida
en un conjunto abierto l R
n
. Sea r
0
un punto de l. Para todos los
vectores / tales que la norma |/| es pequea, con / ,= 0, el punto r
0
+/
tambin pertenece a l. Sin embargo, no tiene sentido escribir
)(r
0
+/) )(r
0
)
/
12
debido a que no existe la divisin por el vector /. Veamos primero el caso de
una variable. En el primer curso de clculo se dene la derivada por
)
0
(r) = lim
|!0
)(r +/) )(r)
/
,
si existe el lmite. En tal caso, sea
q(/) =
)(r +/) )(r)
/
)
0
(r).
Entonces q(/) no est denida para / = 0, sin embargo,
lim
|!0
q(/) = 0.
La ecuacin
) (r +/) ) (r) = )
0
(r) / +/q (/)
tiene sentido solamente cuando / ,= 0. Sin embargo, si denimos q(0) = 0,
entonces dicha ecuacin es cierta tambin para / = 0. La ventaja de esa
ecuacin es que ya no estamos dividiendo entre / y se vale para toda / R, si
la funcin es diferenciable. Extendamos lo anterior al caso multidimensional.
Sea ) : l R
n
R, donde l es abierto. Sean r
0
l y / = (/
1
, . . . , /
n
) tal
que |/| es sucientemente pequea como para que r
0
+/ l. Obsrvese que
r
0
+/ = (r
1
+/
1
, . . . , r
n
+/
n
)
es un punto cercano a r
0
. Podemos decir que ) es continua en r
0
si la
diferencia
)(r
0
+/) )(r
0
)
tiende a cero cuando / tiende a cero.
La condicin adicional que hay que pedir adems de la existencia de todas las
derivadas parciales respecto a todas las variables para tener una buena
denicin de diferenciabilidad se da a continuacin.
Diferenciabilidad de campos escalares. Una funcin ) : l R
n
R es
diferenciable en un punto r
0
del abierto l si existen todas las derivadas
parciales 1
1
)(r
0
), . . . , 1
n
)(r
0
) y si existe una funcin q (q) denida para
vectores / con |/| pequea tal que lim
|!0
q(/) = 0 y
)(r
0
+/) )(r
0
) = \)(r
0
) / +|/| q(/).
Si ) es diferenciable para cada punto de l decimos que ) es diferenciable en l.
Ver [1], [2], [3], [4], [5] y [6].
13
En dos variables la ecuacin de la denicin anterior puede escribirse como
)(r
0
+/, j
0
+/) = )(r
0
, j
0
) +
0)
0r
(r
0
, j
0
) / +
0)
0j
(r
0
, j
0
) / +|/| q(/).
lo cual puede pensarse como una aproximacin lineal al valor de
)(r
0
+/, j
0
+/) mediante la expresin
)(r
0
, j
0
) +
0)
0r
(r
0
, j
0
) / +
0)
0j
(r
0
, j
0
) /
para pequeos valores de (/, /) , ya que lim
(|,|)!(0,0)
q(/) = 0.
Ahora podemos expresar la diferenciabilidad usando el hecho de que
lim
|!0
q(/) = 0 para escribir tal condicin en la siguiente forma:
Nueva denicin de diferenciabilidad.
) : l R
n
R es diferenciable en r
0
si existe \) (r
0
) y si
lim
|!0
1
|/|
[)(r
0
+/) )(r
0
) \)(r
0
) /] = 0.
Demostremos ahora que "diferenciable implica continua".
Teorema. Si ) : l R
n
R es diferenciable en r
0
l, entonces ) es
continua en r
0
.
Demostracin. Veamos primero lo siguiente.
Si para alguna funcin q : l R
n
R se tiene que
lim
|!0
q(/)
|/|
= 0,
la denicin de lmite con - c nos dice que
\- 0 c 0 tal que

q(/)
|/|

< - siempre que |/| < c.

Entonces
\- 0 c 0 tal que [q(/)[ < - |/| siempre que |/| < c.
En particular, lo anterior se cumple para -,c en lugar de -. Por lo tanto,
para toda - 0 existe c 0 tal que
[q(/)[ <
-
c
|/| < - siempre que |/| < c.
14
De ah que
lim
|!0
[q(/)[ = 0.
Apliquemos ahora esta conclusin para demostrar el teorema.
Si ) es diferenciable en r
0
la nueva denicin de diferenciablidad y el resultado
previo implican que
lim
|!0
[)(r
0
+/) )(r
0
) \)(r
0
) /] = 0,
en consecuencia,
lim
|!0
[)(r
0
+/) )(r
0
)] = lim
|!0
\)(r
0
) /,
= \)(r
0
) 0,
= 0,
de donde resulta que
lim
|!0
)(r
0
+/) = ) (r
0
) ,
lo cual nos garantiza que ) es continua en r
0
.
Notacin: El nal de una demostracin ser simbolizado (como arriba) por
.
1.2.7. Regla de la Cadena.
Dada una funcin ) : l R
n
R y una curva A(t) en R
n
podemos formar
la composicin
() A) (t) = ) (A (t))
obteniendo una funcin real de variable real, ) A : R R.
Ejemplo. Sean )(r, j) = c
r
:c:(rj) y A(t) =
_
t
2
, t
3
_
. Entonces
)(A(t)) = c
|
2
:c:(t
5
).
La regla de la cadena para este tipo de composiciones se enuncia y prueba a
continuacin.
Regla de la Cadena (primera versin). Sean ) : l R
n
R
diferenciable en el abierto l y A : 1 R R una curva diferenciable en el
intervalo abierto 1 tal que A(t) l para toda t 1. Entonces
) A : 1 R R es diferenciable y
d
dt
() A) (t) = \)(A(t))
dA
dt
15
Demostracin. Consideremos la diferencia
1 = 1(t, /) = A(t +/) A(t).
En trminos de esta funcin 1 observemos primero que
)(A(t +/)) )(A(t))
/
=
)(A(t) +1) )(A(t))
/
.
Como ) es diferenciable tenemos que, por denicin,
)(A +1) )(A) = \)(A) 1 +|1| q(1),
donde
lim
1!0
q(1) = 0.
Sustituyendo 1 obtenemos:
)(A(t +/)) )(A(t))
/
=
\)(A (t)) 1 +|1| q(1)
/
,
= \)(A (t))
A(t +/) A(t)
/

_
_
_
_
A(t +/) A(t)
/
_
_
_
_
q(1),
y tomando el lmite cuando / 0, resulta lo siguiente
d
dt
) (A (t)) = \)(A (t)) A
0
(t) |A
0
(t)| lim
|!0
q(1).
Ahora, cuando / 0 se tiene que 1 = [A(t +/) A(t)] 0, por lo tanto
lim
|!0
q(1) = lim
1!0
q(1) = 0.
De ah que
d
dt
() A) (t) = \)(A(t))
dA
dt
tal como queramos demostrar.
Pongamos esta regla de la cadena en trminos de las coordenadas. Si
A = (r
1
, . . . , r
n
), entonces
d()(A(t)))
dt
=
0)
0r
1
dr
1
dt
+ +
0)
0r
n
dr
n
dt
.
Si ) es una funcin de dos variables (r, j) lo anterior se escribe ms
frecuentemente como
d()(A(t)))
dt
=
0)
0r
dr
dt
+
0)
0j
dj
dt
.
16
Esto puede aplicarse a situaciones ms generales donde r, j dependan de ms
de una variable. Por ejemplo, si
r = ,(t, n), j = c(t, n)
son funciones diferenciables de las dos variables t, n, entonces la composicin
de )(r, j) con ,, c puede escribirse como una funcin
q(t, n) = )(,(t, n), c(t, n)).
Si mantenemos ja la variable n podemos calcular la derivada parcial de q
respecto a t utilizando la regla de la cadena:
0q
0t
=
0)
0r
0r
0t
+
0)
0j
0j
0t
.
Ejemplo. Sea )(r, j) = r
2
+ 2rj, y sean r = r cos 0, j = r :c: 0. La
composicin es
q (r, 0) = )(r(r, 0) , j (r, 0)).
Entonces
0r
0r
= cos 0,
0j
0r
= :c: 0,
0r
00
= r :c: 0,
0j
00
= r cos 0,
y de ah que
0q
0r
=
0)
0r
0r
0r
+
0)
0j
0j
0r
= (2r + 2j)(cos 0) + 2r(:c: 0),
0q
00
=
0)
0r
0r
00
+
0)
0j
0j
00
= (2r + 2j)(r :c: 0) + 2r(r cos 0).
Si quisiramos estas derivadas solamente en trminos de r y 0, tendramos que
sustitur r = r cos 0 y j = r :c: 0 en las expresiones obtenidas.
Ejemplo. Puede ocurrir que r, j no se usen para denotar la primera y
segunda variables de una funcin ). Por ejemplo, si
n = )(r
2
j, rj),
entonces, para encontrar
0n
0r
pongamos
: = r
2
j, t = rj.
17
Entonces, n = )(:(r, j), t(r, j)) y as,
0n
0r
=
0)
0:
0:
0r
+
0)
0t
0t
0r
,
= 2r
0)
0:
+j
0)
0t
.
Similarmente,
0n
0j
=
0)
0:
0:
0j
+
0)
0t
0t
0j
,
=
0)
0:
+r
0)
0t
.
De las dos ecuaciones anteriores se pueden despejar las funciones
J}
Js
y
J}
J|
resolviendo el sistema para obtener, por ejemplo,
0)
0t
=
1
j + 2r
2
_
0n
0r
+ 2r
0n
0j
_
.
Ejemplo. Sea )(r, j, .) = q(r
2
3.j +r.), donde q es una funcin
diferenciable de una variable. Entonces se puede escribir
0)
0r
= q
0
_
r
2
3.j +r.
_
(2r +.) ,
donde hemos denotado la derivada de q por q
0
como es usual en clculo de una
variable. No escribimos
dq
dr
porque la letra r ya tiene otro signicado en la
expresin q
_
r
2
3.j +r.
_
. Si queremos expresar la derivada de q como un
cociente diferencial en lugar de la "prima", podemos hacer
n = r
2
3.j +r.
para tener )(r, j, .) = q(n(r, j, .)), y de ah,
0)
0r
=
dq
dn
0n
0r
,
=
dq
dn
(2r +.) .
En general, si /(r, j, .) es una funcin de r, j, ., y q es una funcin de una
variable, podemos formar la composicin
)(r, j, .) = q(/(r, j, .)),
y de ah,
0)
0r
= q
0
(/(r, j, .))
0/
0r
.
18
Ejemplo. Sea q(t, r, j) = )
_
t
2
r, tj
_
. Haciendo
n = t
2
r, = tj,
podemos escribir
q(t, r, j) = )(n(t, r, j), (t, r, j)),
y de ah que
0q
0t
=
0)
0n
0n
0t
+
0)
0
0
0t
,
= 2tr )
u
+j )
u
,
donde hemos denotado las derivadas parciales de ) con subndices.
1.2.8. Planos tangentes a supercies de nivel.
Sea ) (A) una funcin diferenciable de A = (r, j, .) R
3
y sea c un nmero
real.
Denicin. El conjunto de puntos o
c
=
_
A R
3
[ ) (A) = c
_
donde
\)(A) ,= 0 es una supercie. En otras palabras: una supercie es un
conjunto de nivel de una funcin diferenciable de 3 variables donde no se anula
el gradiente.
Ver [2].
Decimos que una curva diferenciable A(t) vive en la supercie o
c
si
)(A(t)) = c. Esto signica que todos los puntos de la curva satisfacen la
ecuacin que dene la supercie de nivel c. Para cualquier curva que vive en
una supercie de nivel, la regla de la cadena nos asegura que
\)(A(t)) A
0
(t) = 0.
Lo anterior tiene la siguiente consecuencia inmediata si A
0
(t) ,= 0: el gradiente
en un punto X(t
0
) es ortogonal a cualquier vector tangente X(t
0
) de cualquier
curva X(t) que vive en una supercie de nivel. Lo anterior motiva la siguiente
denicin.
Denicin. Para una funcin diferenciable de tres variables ) se dene el
plano tangente a una supercie de nivel de ) en un punto 1 por el plano que
pasa por 1 y es ortogonal al vector \)(1), si este gradiente no se anula. Para
los puntos donde \)(1) = 0, el plano tangente no est denido.
Ver [2] y [6].
19
La ecuacin del plano tangente a una supercie de nivel en uno de sus puntos
1 es entonces de la forma siguiente:
\)(1) (A 1) = 0.
Ejemplo. Encontrar el plano tangente a la supercie
r
2
+j
2
+.
2
= 3
en el punto (1, 1, 1) .
Sea )(r, j, .) = r
2
+j
2
+.
2
. Entonces la supercie dada es el nivel 3 de ),
una esfera de radio
_
3 con centro en el origen de R
3
. Como
\)(r, j, .) = (2r, 2j, 2.), vemos que en el punto 1 = (1, 1, 1) de esta esfera,
\)(1) = (2, 2, 2), luego la ecuacin del plano tangente buscado es
(2, 2, 2) (r 1, j 1, . 1) = 0,
2r + 2j + 2. 6 = 0.
1.2.9. Planos tangentes a grcas de funciones.
Si . = q(r, j) dene una funcin de dos variables, la grca de q se puede ver
como una supercie de nivel de la funcin de tres variables ) denida por
)(r, j, .) = q(r, j) ., y el plano tangente a la grca de q es el plano
tangente de la supercie de nivel cero de ).
Ejemplo. Encontrar el plano tangente a la supercie
. = r
2
+j
2
en el punto (1, 2, 5).
Sea )(r, j, .) = r
2
+j
2
.. Entonces \)(r, j, .) = (2r, 2j, 1), y por lo
tanto, \)(1, 2, 5) = (2, 4, 1). As que la ecuacin pedida es
(2, 4, 1) (r 1, j 2, . 5) = 0,
2r + 4j . 5 = 0.
Se puede dar una frmula general para la ecuacin del plano tangente a la
grca de una funcin de dos variables denida por . = )(r, j) como sigue.
Sea
1(r, j, .) = )(r, j) ..
20
Entonces la grca es la supercie de nivel cero de 1 y as, el plano tangente
en un punto
(r
0
, j
0
, .
0
) , .
0
= )(r
0
, j
0
)
de la grca de ) est dado por:
\1(r
0
, j
0
, .
0
) (r r
0
, j j
0
, . .
0
) = 0,
esto es,
()
r
(r
0
, j
0
), )

(r
0
, j
0
), 1) (r r
0
, j j
0
, . .
0
) = 0,
)
r
(r
0
, j
0
) (r r
0
) +)

(r
0
, j
0
) (j j
0
) (. .
0
) = 0,
o bien,
. = )(r
0
, j
0
) +
0)
0r
(r
0
, j
0
) (r r
0
) +
0)
0j
(r
0
, j
0
) (j j
0
),
de donde se puede interpretar al plano tangente como la aproximacin de
primer orden a la grca en el punto de tangencia, esto signica que el plano
tangente representa al polinomio de primer grado en dos variables que mejor
se aproxima a la grca de la funcin en dicho punto. Si la funcin es lineal,
ambas cosas coinciden. Si la funcin no es lineal y se quiere obtener una mejor
aproximacin que la de primer orden, es necesario desarrollar un polinomio
cuadrtico en dos variables. Haremos eso en una seccin posterior cuando
hablemos del polinomio de Taylor de segundo orden. Podemos decir que el
plano tangente es el polinomio de Taylor de primer orden de la funcin.
La tima ecuacin puede desarrollarse en la forma
ar +/j +c. +d = 0,
donde los coecientes son:
a =
0)
0r
(r
0
, j
0
) , / =
0)
0j
(r
0
, j
0
) , c = 1,
d = .
0
r
0
0)
0r
(r
0
, j
0
) j
0
0)
0j
(r
0
, j
0
) .
Tambin es posible obtener la ecuacin del plano tangente usando derivadas
parciales respecto a otros pares de variables distintos del par (r, j).
Ejemplo. Encontrar el plano tangente a la supercie
r = c
2:
en el punto (1, 1, 2).
21
Sea q(j, .) = c
2:
. Entonces la ecuacin del plano tangente est dada por
r = q(j
0
, .
0
) +
0q
0j
(j
0
, .
0
) (j j
0
) +
0q
0.
(j
0
, .
0
) (. .
0
),
donde (j
0
, .
0
) = (1, 2). Luego,
0q
0j
= 2c
2:
,
0q
0j
(1, 2) = 2c
0
= 2,
0q
0.
= c
2:
,
0q
0.
(1, 2) = c
0
= 1,
y de ah que el plano pedido sea
r = 1 + 2 (j 1) + (1) (. 2) ,
o bien,
r 2j +. 1 = 0.
1.2.10. Derivadas direccionales.
Sea ) una funcin diferenciable denida en un conjunto abierto l R
n
. Dado
un punto 1 l y un vector unitario \ , la lnea recta que pasa por 1 con
direccin \ est parametrizada por A(t) = 1 +t\ . Como
dA
dt
= \ , la regla
de la cadena implica que
d
dt
)(1 +t\ ) = \) (1 +t\ ) \,
luego, para t = 0 resulta
d
dt
[
|=0
)(1 +t\ ) = \)(1) \.
Esta derivada representa la razn de cambio de la restriccin de la funcin ) a
la lnea recta que pasa por 1 con direccin \ . Lo anterior nos induce a denir
el siguiente concepto.
Denicin. La derivada direccional de una funcin ) : l R
n
R en un
punto 1 del abierto l en la direccin de un vector unitario \ se dene por
1
\
)(1) =
d
dt
[
|=0
)(1 +t\ ).
22
Ver [1] y [2].
Por lo visto arriba resulta que esta derivada direccional se puede calcular por el
producto punto del vector direccin por el gradiente de la funcin en el punto.
Obsrvese que las derivadas parciales son las derivadas direccionales en las
direcciones de los vectores bsicos unitarios ortogonales c
I
= (0, . . . , 1, . . . , 0),
donde el 1 se encuentra en el lugar i y los dems son ceros. Por ejemplo,
1
t1
)(1) =
d
dt
[
|=0
)(1 +tc
1
),
=
d
dt
[
|=0
)((j
1
, . . . , j
n
) +t (1, 0, . . . , 0))
=
d
dt
[
|=0
() (j
1
+t, j
2
, . . . , j
n
)) ,
= lim
|!0
) (j
1
+/, j
2
, . . . , j
n
) ) (j
1
, j
2
, . . . , j
n
)
/
,
=
0)
0r
1
(j
1
, . . . , j
n
).
En general, 1
ti
)(1) =
0)
0r
I
(j
1
, . . . , j
n
).
Ejemplo. Sean )(r, j) = r
2
+j
3
, \ = (1, 2). Encontrar la derivada
direccional de ) en el punto (1, 3) en la direccin de \. Como |\| =
_
5, el
vector unitario en la direccin de \ es
\ =
1
_
5
\ =
_
1
_
5
,
2
_
5
_
.
El gradiente es
\)(r, j) =
_
2r, 3j
2
_
,
luego \)(1, 3) = (2, 27), por lo tanto
1
\
)(1, 3) = (2, 27)
_
1
_
5
,
2
_
5
_
,
=
2
_
5
+
54
_
5
=
52
_
5
.
Si la derivada direccional de una funcin ) mide la razn de cambio de ) en un
punto y en una direccin, cul es la direccin de mximo crecimiento de ) a
partir de un punto? La respuesta es el gradiente en ese punto, si es que no se
anula, por lo siguiente. La derivada direccional est dada por
1
\
)(1) = \)(1) \,
23
y como \ es unitario,
1
\
)(1) = |\)(1)| |\ | cos 0,
= |\)(1)| cos 0,
donde 0 es el ngulo entre \)(1) y \ . De ah resulta que 1
\
)(1) alcanza su
mayor valor posible cuando cos 0 es mximo. Como 1 < cos 0 < 1, este
mximo es 1 y se alcanza cuando 0 = 0

, es decir, cuando \ est en la

direccin de \)(1). Cuando 0 = 180

se tiene la direccin de mnimo

crecimiento de la funcin, \ = \)(1). Tambin se dice que \)(1) es la
direccin de mximo decrecimiento de la funcin en 1. Entonces la razn de
mximo crecimiento en 1 es la norma del gradiente en 1 y su negativo es la
razn de mximo decrecimiento. Por ejemplo, si T(r, j, .) mide la
temperatura en un espacio determinado, un mosquito que sienta calor en un
punto de su vuelo y quiera enfriarse lo ms rpido posible, deber moverse en
la direccin opuesta al gradiente de la temperatura en dicho punto, \T(1).
1.2.11. Derivadas de orden superior.
Sea ) : l R
2
R una funcin de dos variables denida en un abierto l del
plano de coordenadas (r, j). Supngase que existen sus derivadas parciales
respecto a r y a j en todo punto de l. Entonces 1
r
) y 1

) son funciones
denidas en el mismo abierto l, y como tales podemos preguntarnos si existen
sus derivadas parciales. En caso armativo las llamaremos derivadas parciales
de segundo orden, o tambin, segundas derivadas parciales. Puede haber
cuatro, las cuales se pueden denotar por:
1
r
1
r
) =
0
0r
_
0)
0r
_
=
0
2
)
0r
2
= )
rr
,
1

1
r
) =
0
0j
_
0)
0r
_
=
0
2
)
0j 0r
= )
r
,
1
r
1

) =
0
0r
_
0)
0j
_
=
0
2
)
0r 0j
= )
r
,
1

) =
0
0j
_
0)
0j
_
=
0
2
)
0j
2
= )

,
o tambin por 1
11
), 1
12
), 1
21
), 1
22
).
Ejemplo. Sea )(r, j) = :c:(rj). Entonces
0)
0r
= j cos(rj),
0)
0j
= rcos(rj),
24
y de ah que
0
2
)
0r
2
= j :c: (rj) j = j
2
:c: (rj),
0
2
)
0j0r
= j :c: (rj) r + cos(rj) = rj :c:(rj) + cos(rj),
0
2
)
0r0j
= r :c: (rj) j + cos(rj) = rj :c:(rj) + cos(rj),
0
2
)
0j
2
= r :c: (rj) r = r
2
:c: (rj).
Obsrvese que las derivadas parciales mixtas son iguales, esto es,
0
2
)
0j0r
=
0
2
)
0r0j
. Se puede demostrar que lo anterior se cumple siempre que
dichas derivadas parciales de segundo orden existan y sean continuas.
Similarmente, para una funcin de tres variables )(r, j, .) se puede hablar de
derivadas parciales de orden superior como por ejemplo,
1
:
1
r
) =
0
0.
_
0)
0r
_
=
0
2
)
0. 0r
= )
:r
,
1
r
1
:
1
r
) =
0
0r
_
0
0.
_
0)
0r
__
=
0
3
)
0r 0. 0r
= )
r:r
,
etc...
Si existen todas las derivadas parciales hasta orden 3 y son continuas, entonces
tambin resultan iguales las mixtas, como por ejemplo,
0
3
)
0r 0.
2
= 1
r
1
:
1
:
) = 1
:
1
r
1
:
) = 1
:
1
:
1
r
) =
0
3
)
0.
2
0r
,
etc...
Se dice que una funcin es de clase C
:
para r = 0, 1, 2, . . . , si existen todas las
derivadas parciales hasta orden r y son continuas. La clase C
0
est formada
por las funciones continuas. Uno de los teoremas conocidos es que si una
funcin es de clase C
|
, entonces es de clase C
:
para toda r _ /. En particular,
si una funcin ) es de clase C
1
(existen las primeras derivadas parciales y son
continuas) entonces es continua. Lo anterior se debe a dos hechos conocidos:
(1) si ) es de clase C
1
entonces es diferenciable,
(2) la diferenciabilidad implica la continuidad.
Las pruebas de estos hechos requieren algunos conocimientos de lgebra lineal
que an no han sido expuestos a los estudiantes de este curso. Por tal razn
no se dan aqu. El lector interesado puede encontrar demostraciones en [1], [3]
y [4].
25
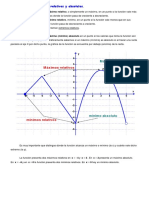
1.2.12. Mximos y mnimos de funciones de dos
variables
Denicin. Para una funcin ) denida en un abierto l del :-espacio
Euclidiano R
n
, un punto j l se dice crtico si todas las primeras derivadas
parciales de ) se anulan en j:
0)
0r
1
(j) =
0)
0r
2
(j) = =
0)
0r
n
(j).
Ver [1], [2], [3], [4] y [5].
Ejemplo. Encontrar los puntos crticos de )(r, j) = c
(r
2
+
2
)
.
Como
0)
0r
= 2rc
(r
2
+
2
)
, y
0)
0j
= 2jc
(r
2
+
2
)
, entonces el nico punto
crtico es el (0, 0), ya que las exponenciales nunca se anulan.
Del clculo I sabemos de la existencia de puntos donde la derivada es cero sin
que eso implique un mximo o un mnimo. Por ejemplo, el origen es un punto
crtico de )(r) = r
3
, siendo este un punto de inexin. Algo similar ocurre en
varias variables. Por ejemplo, para )(r, j) = r
2
j
2
tenemos que las primeras
derivadas parciales )
r
= 2r, )

= 2j, se anulan en el origen (0, 0). Sin

embargo, en la direccin r (cuando j = 0) se tiene un mnimo, mientras que en
la direccin j (cuando r = 0) se tiene un mximo. Luego no existe una bola
abierta 1
:
(0, 0) con centro en el origen tal que todos los valores de la funcin
sean positivos para todo punto de 1
:
(0, 0) ni tampoco son negativos para todo
punto de la misma bola. Se dice que el origen es un punto de inexin de la
funcin ).
Denicin. Sea ) : l R
n
R denida en un abierto l. Decimos que un
punto j l es un mximo local de ) si existe una bola abierta 1
:
(j) de algn
radio - 0 tal que
)(j) _ )(r) \r 1
:
(j).
Anlogamente, decimos que j es un mnimo local de ) si existe alguna bola
abierta 1
:
(j) de algn radio - 0 tal que
)(j) _ )(r) \r 1
:
(j).
Si las anteriores desigualdades se cumplen para toda r en el dominio de )
entonces les llamaremos mximo global y mnimo global, respectivamente.
Ver [1], [2], [3], [4] y [5].
26
Ejemplo. Para )(r, j) = r
2
+j
2
el origen es un mnimo global, mientras que
para )(r, j) = r
2
j
2
, el origen es un mximo global.
Como ya sabemos, no todo punto crtico es un extremo (mximo o mnimo)
local, lo que s se cumple siempre en dominios abiertos es que un extremo local
es un punto crtico, como vamos a demostrar enseguida.
Teorema. Sea ) : l R
n
R una funcin diferenciable denida en un
abierto l del :-espacio Euclidiano. Si j l es un mximo o mnimo local de
), entonces j es un punto crtico.
Demostracin. Sea un vector distinto de cero. Para j l y t R
pequeo, j +t pertenece al abierto l. Supongamos que j es un mximo local
de ). Entonces existe - 0 tal que para toda t (-, -),
)(j) _ )(j +t)
en cualquier direccin . Sea q : (-, -) R denida por
q(t) = )(j +t).
Como q es la composicin de una funcin diferenciable con una curva
diferenciable (la recta j +t), la regla de la cadena implica que q es
diferenciable y
q
0
(t) = \)(j +t) ,
adems, q(0) = )(j) _ q(t) para toda t (-, -), luego q tiene un mximo
local en t = 0. Por clculo I sabemos que q
0
(0) = 0 y de ah que
\)(j) = 0
para todo vector . Por lo tanto \)(j) es el vector cero, es decir, todas las
derivadas parciales de ) se anulan en el punto j. Lo mismo ocurre si j es un
mnimo local de ).
Una consecuencia inmediata del teorema anterior es la siguiente: si existen
mximos o mnimos locales de una funcin en un abierto, se encuentran entre
los puntos crticos.
Ahora, un criterio que ayude a determinar la naturaleza de los puntos crticos
dentro de un dominio abierto de una funcin de dos variables se basa en el
polinomio de Taylor de segundo orden. En el clculo de funciones de una
variable el teorema de Taylor arma que una funcin diferenciable de clase C
:
se puede aproximar en un punto interior a de su dominio abierto por
)(a +/) = )(a) +)
0
(a)/ +
)
(2)
(a)
2!
/
2
+ +
)
(r1)
(a)
(r 1)!
/
:1
+1,
27
donde 1 es llamado el residuo en esta aproximacin a ) por un polinomio de
grado r 1 en la vecindad de un punto a. Veamos cmo podemos generalizar
esta frmula para funciones de dos variables. Sean j = (a, /) y H = (/, /), con
j en un abierto l R
2
donde est denida una funcin ) de clase C
:
, r _ 3.
Sea
q(t) = )(j +tH) = )(a +t/, / +t/)
para t [0, 1], suponiendo que j +tH l para estos valores de t. Entonces
q(1) = )(j +H) j q(0) = )(1).
Podemos aplicar el teorema de Taylor en una variable a la funcin q para
obtener:
q(1) = q(0) +q
0
(0) +
q
00
(0)
2!
+ +1.
Hagamos ahora
r = a +t/, j = / +t/.
Por la regla de la cadena,
q
0
(t) =
0)
0r
0r
0t
+
0)
0j
0j
0t
=
0)
0r
/ +
0)
0j
/.
Para la segunda derivada, debemos encontrar la derivada respecto a t de cada
una de las funciones )
r
y )

. Aplicando nuevamente la regla de la cadena,

d
dt
_
0)
0r
_
=
0
2
)
0r
2
dr
dt
+
0
2
)
0j 0r
dj
dt
=
0
2
)
0r
2
/ +
0
2
)
0j 0r
/.
Similarmente,
d
dt
_
0)
0j
_
=
0
2
)
0r 0j
/ +
0
2
)
0j
2
/.
Usando lo anterior, resulta:
q
00
(t) = /
_
0
2
)
0r
2
/ +
0
2
)
0j 0r
/
_
+/
_
0
2
)
0r 0j
/ +
0
2
)
0j
2
/
_
= /
2
0
2
)
0r
2
+ 2//
0
2
)
0r 0j
+/
2
0
2
)
0j
2
.
En consecuencia,
)(a+/, /+/) = )(a, /)+)
r
(a, /)/+)

(a, /)/+
1
2
_
)
rr
(a, /)/
2
+ 2)
r
(a, /)// +)

(a, /)/
2

+1,
28
donde 1 es el residuo.
Si j = (a, /) es un punto crtico, las primeras derivadas parciales se anulan, de
ahi que
)(a +/, / +/) )(a, /) =
1
2
_
)
rr
(a, /)/
2
+ 2)
r
(a, /)// +)

(a, /)/
2

+1.
De lo anterior vemos que la forma cuadrtica
Q = )
rr
(a, /)/
2
+ 2)
r
(a, /)// +)

(a, /)/
2
es importante para determinar el signo de la diferencia
)(a +/, / +/) )(a, /), lo cual puede dar informacin acerca de la naturaleza
del punto crtico (a, /). Por ejemplo, si
)(a +/, / +/) _ )(a, /)
para todo punto (/, /) sucientemente cercano al punto crtico (a, /), entonces
(a, /) es un mximo local de ). Si la desigualdad es _ en lo anterior, (a, /) es
un mnimo local de ).
Pongamos las segundas derivadas parciales en un arreglo matricial de 2 2
como sigue:
_
)
rr
)
r
)
r
)

_
.
Si ) es de clase C
3
al menos, )
r
= )
r
. En tal caso llamemos al
determinante de esta matriz:
= )
rr
)

)
r
)
r
= )
rr
)

)
2
r
.
Esta funcin, llamada el hessiano de ) es muy til en el siguiente criterio para
determinar la naturaleza de los puntos crticos de una funcin de dos variables.
Criterio de Mximos y Mnimos. Sea ) : l R
2
R una funcin de
clase C
:
, r _ 3, denida en un abierto l y sea j l un punto crtico de ).
Entonces:
(i) )
rr
(j) < 0 y (j) 0 == j es un mximo local de ),
(ii) )
rr
(j) 0 y (j) 0 == j es un mnimo local de ),
(iii) (j) < 0 == j es un punto de inexin de ).
Cuando (j) = 0 este criterio no da informacin.
29
Demostracin. Hagamos a
11
= )
rr
(j), a
12
= )
r
(j) = )
r
(j), a
22
= )

(j).
Entonces, como ya vimos, para cualquier punto (/, /) sucientemente cercano
a j = (a, /), podemos decir que
)(a +/, / +/) )(a, /)
~
=
1
2
_
a
11
/
2
+ 2a
12
// +a
22
/
2

,
y de ahi que el signo de la diferencia )(a +/, / +/) )(a, /) est determinado
por el signo de la forma cuadrtica Q = a
11
/
2
+ 2a
12
// +a
22
/
2
. Ahora,
factorizando y completando cuadrados,
a
11
/
2
+ 2a
12
// +a
22
/
2
= a
11
_
/
2
+
2a
12
a
11
// +
a
22
a
11
/
2
_
,
= a
11
_
/
2
+
2a
12
a
11
// +
a
2
12
a
2
11
/
2

a
2
12
a
2
11
/
2
+
a
22
a
11
/
2
_
,
= a
11
_
_
/ +
a
12
a
11
/
_
2
+ (a
11
a
22
a
2
12
)
/
2
a
2
11
_
.
De donde vemos que Q 0 si a
11
0 y a
11
a
22
a
2
12
0, mientras que Q < 0
si a
11
< 0 y a
11
a
22
a
2
12
0. Esto prueba los incisos (i) y (ii). Dejamos como
ejercicio el resto de la prueba.
Para nalizar esta seccin vamos a enunciar un teorema importante para
completar la teora de mximos y mnimos en varias variables, cuya prueba
requiere algunos conocimientos de topologa por lo cual no la daremos aqu.
Teorema. Sea ) : R
n
R una funcin continua denida en un conjunto
cerrado y acotado . Entonces ) alcanza su mximo y su mnimo globales en
.
As, cuando se estn buscando los extremos de una funcin dada, primero se
deben encontrar los puntos crticos en el interior abierto del dominio de la
funcin. Si un mximo o mnimo locales ocurre en este interior abierto,
sabemos que debe estar entre estos puntos crticos. Luego, se deben investigar
los puntos de la frontera del dominio de la funcin. Generalmente, el nmero
de variables en la frontera puede reducirse mediante alguna parametrizacin.
Entonces puede aplicarse la tcnica de puntos crticos a la frontera en un
problema de menos dimensiones.
Ejemplo. Sea )(r, j) = c
(r
2
+
2
)
. Esta funcin tiende a cero cuando (r, j) se
aleja cada vez ms del origen. Considrese alguna 2-bola cerrada

1
1
(0, 0) del
plano del dominio de ) con centro en el origen (0, 0) y radio 1 grande. Por el
criterio de mximos y mnimos sabemos que ) alcanza su mximo en esta bola
cerrada (y acotada por 1). Como los valores de la funcin en la frontera de la
bola son pequeos, se deduce que este mximo debe ser un punto del interior,
30
esto es, de la bola abierta 1
1
(0, 0). De ah que este mximo debe ser un
punto crtico. Como
0)
0r
= 2rc
(r
2
+
2
)
,
0)
0j
= 2jc
(r
2
+
2
)
,
resulta que el nico punto crtico es el origen (0, 0). Por lo tanto la funcin
alcanza su mximo global en el (0, 0) y vale )(0, 0) = 1. El mnimo global en
esta bola cerrada de radio 1 es, debido a la simetra de la funcin respecto al
origen, el valor en cualquier punto de la frontera, esto es, c
1
2
. Si extendemos
el dominio a todo el plano R
2
, vemos que esta ) no tiene mnimo, pues
lim
1!1
c
1
2
= 0.
1.3. Campos Vectoriales.
1.3.1. La derivada de un campo vectorial.
Comenzaremos esta seccin dando una interpretacin distinta de la
diferenciacin de una funcin real-valuada denida en un conjunto abierto del
:-espacio, ) : l R
n
R, como sigue. Anteriormente usamos el gradiente
\) en un punto A l para decir que ) es diferenciable en A si se cumple que
)(A +H) )(A) = \)(A) H +|H| q(H)
para H pequeo donde lim
1!0
q(H) = 0.
Ahora, el producto punto \)(A) H se puede interpretar, si se escribe al
vector H = (H
1
, . . . , H
n
) como vector columna, como el siguiente producto de
matrices:
(1
1
)(A) 1
n
)(A))
_
_
_
H
1
.
.
.
H
n
_
_
_,
donde 1
I
) =
0)
0r
I
.
Con esta interpretacin podemos decir que ) es diferenciable si existe una
matriz de 1 : y una funcin q de manera que, para vectores H de norma
pequea, se puede escribir
)(A +H) )(A) = H +|H| q(H),
donde lim
1!0
q(H) = 0, y = (1
1
)(A) 1
n
)(A)).
31
En el caso ms general de una funcin 1 : l R
n
R
n
, que es llamado un
campo vectorial se da la siguiente
Diferenciabilidad de campos vectoriales. Una funcin
1 : l R
n
R
n
de un abierto l de R
n
es diferenciable en A l si
existe una matriz de :: y existe una funcin G denida para vectores H
de norma pequea, tales que
1(A +H) 1(A) = H +|H| q(H),
donde lim
1!0
G(H) = 0.
Ver [2], [3], [4] y [6].
1.3.2. La matriz Jacobiana.
En cursos ms avanzados de clculo se ve que la matriz que entra en la
denicin de diferenciabilidad de campos vectoriales, est determinada de
manera nica por lo que se llama la Jacobiana de 1, la cual es la matriz de
las derivadas parciales de todas las : funciones componentes de 1 respecto a
todas las : variables. Si se escribe 1 como
1(r
1
, . . . , r
n
) = ()
1
(r
1
, . . . , r
n
) , . . . , )
n
(r
1
, . . . , r
n
)) ,
entonces la matriz Jacobiana de 1 se dene por:
J
J
(A) =
_
_
_
_
_
_
_
_
_
_
_
_
0)
1
0r
1
0)
1
0r
2

0)
1
0r
n
0)
2
0r
1
0)
2
0r
2

0)
2
0r
n
.
.
.
.
.
.
.
.
.
0)
n
0r
1
0)
n
0r
2

0)
n
0r
n
_
_
_
_
_
_
_
_
_
_
_
_
=
_
0)
I
0r

_
1In, 1n
donde cada una de las derivadas parciales est evaluada en A. En el caso de
un campo vectorial de R
2
en R
2
, denido por 1(r, j) = () (r, j) , q(r, j)), la
matriz Jacobiana es
J
J
(r, j) =
_
_
_
_
_
0)
0r
0)
0j
0q
0r
0q
0j
_
_
_
_
_
.
1.3.3. Ejemplos en dimensiones 1, 2 y 3.
32
Ejemplo. Sea 1 : R
2
R
2
denida por
1(r, j) =
_
r
2
+j
2
, c
r
_
= ()(r, j), q(r, j)) .
La matriz Jacobiana J
J
(r, j) es
_
_
_
_
_
0)
0r
0)
0j
0q
0r
0q
0j
_
_
_
_
_
=
_
2r 2j
jc
r
rc

_
.
As, por ejemplo, para A = (1, 1), encontramos
J
J
(1, 1) =
_
2 2
c c
_
.
Ejemplo. Sea 1 : R
2
R
3
denida por
1(r, j) =
_
rj, :c: r, r
2
j
_
.
La matriz Jacobiana J
J
(r, j) es
_
_
j r
cos r 0
2rj r
2
_
_
.
Luego, para A = (, ,2), tenemos
J
J
(, ,2) =
_
_
,2
1 0

2
_
_
.
Ejemplo. Sea 1 : R
3
R
3
denida por
1(r, j, .) = (r +j +., rj +r. +j., rj.) .
La matriz Jacobiana J
J
(r, j, .) es
_
_
1 1 1
j +. r +. r +j
j. r. rj
_
_
.
Luego, para A = (1, 1, 0), tenemos
J
J
(1, 1, 0) =
_
_
1 1 1
1 1 0
0 0 1
_
_
.
33
A la matriz Jacobiana de una funcin ) : R
n
R
n
se le llama tambin la
derivada de ) y se denota por 1). Se puede decir que la derivada, en el caso
ms general, es una matriz de ::. Para campos escalares es la matriz de
1 : representada por el vector gradiente. Para funciones reales de variable
real es la matriz de 1 1 denida por el nmero real asociado a la derivada del
clculo elemental.
1.3.4. Regla de la Cadena.
En la seccin de campos escalares vimos la regla de la cadena para la
composicin ) c de una curva c : 1 R R
n
seguida de un campo escalar
) : R
n
R, y encontramos frmulas a partir de ah para expresar derivadas de
composiciones ms generales. Dichas frmulas se deducen del caso ms
general, que puede enunciarse como sigue.
Regla de la Cadena General. Sean ) : l R
n
R
n
y
q : \ R
n
R

dos funciones tales que )(l) \ de tal manera que q )

est denida. Si ) es diferenciable en x
0
y q es diferenciable en )(x
0
),
entonces q ) es diferenciable en x
0
y se cumple que:
1(q )) (x
0
) = 1q ()(x
0
)) 1)(x
0
),
donde el lado derecho es el producto de las matrices jacobianas
correspondientes.
1.3.5. Ejemplos en dimensiones 1, 2 y 3.
Corolario. Sea q (r, j, .) = (n(r, j, .) , (r, j, .) , n(r, j, .)) una
transformacin diferenciable de un conjunto abierto de R
3
en R
3
y sea
) : R
3
R diferenciable. Si /(r, j, .) = )(n(r, j, .) , (r, j, .) , n(r, j, .)),
entonces
0/
0r
=
0)
0n
0n
0r
+
0)
0
0
0r
+
0)
0n
0n
0r
,
con frmulas similares para
0/
0j
,
0/
0.
. Es comn abusar de la notacin y
escribir
0)
0r
para
0/
0r
, por ejemplo.
Demostracin. La prueba se sigue de la Regla de la Cadena y del producto
de las matrices jacobianas correspondientes a las funciones involucradas:
1/(r, j, .) = 1)(n, , n)1q(r, j, .),
34
que es el producto de matrices siguiente:
_
0/
0r
0/
0j
0/
0.
_
=
_
0)
0n
0)
0
0)
0n
_
_

_
0n
0r
0n
0j
0n
0.
0
0r
0
0j
0
0.
0n
0r
0n
0j
0n
0.
_

_
,
de donde resultan las frmulas.
El lector puede comprobar que la regla de la cadena estudiada en la seccin de
campos escalares es un caso particular de la Regla de la Cadena General.
Ejemplo. Para ) (n, , n) = n
2
+
2
n, donde n = r
2
j, = j
2
, n = c
r:
,
se tiene que
/(r, j, .) = ) (n(r, j, .) , (r, j, .), n(r, j, .))
= r
4
j
2
+j
4
c
r:
.
As,
0/
0r
= 4r
3
j
2
+.c
r:
.
Por otro lado,
0)
0n
0n
0r
+
0)
0
0
0r
+
0)
0n
0n
0r
= 2n(2rj) + 2 0 +.c
r:
=
_
2r
2
j
_
(2rj) +.c
r:
= 4r
3
j
2
+.c
r:
,
con lo cual vericamos la validez de regla de la cadena para estas funciones.
Ejemplo. Dadas ) (r, j) =
_
r
2
+ 1, j
2
_
y q(n, ) =
_
n +, n,
2
_
, calcular
la derivada de q ) en el punto (1, 1).
1q(n, ) =
_

_
0q
1
0n
0q
1
0
0q
2
0n
0q
2
0
0q
3
0n
0q
3
0
_

_
=
_
_
1 1
1 0
0 2
_
_
,
y
35
1)(r, j) =
_
2r 0
0 2j
_
.
Entonces resulta
1(q ))(1, 1) = 1q(2, 1)1)(1, 1) =
_
_
1 1
1 0
0 2
_
_
_
2 0
0 2
_
=
_
_
2 2
2 0
0 4
_
_
.
36
1.3.6. Funciones inversas y funciones implcitas.
Sea 1 : l R
n
R
n
una funcin denida en un abierto l mediante
1(A) = ()
1
(A), . . . , )
n
(A)).
Si todas las derivadas parciales de todas las funciones componentes )
I
existen
y son continuas, se dice que 1 es de clase C
1
.
Denicin. Una funcin 1 : l R
n
R
n
de clase C
1
en un abierto l se
dice que es invertible en l si la imagen 1(l) es un abierto \ y si adems
existe una funcin G : \ l de clase C
1
tal que G es la funcin inversa de 1:
G 1 : l l es la identidad en l,
1 G : \ \ es la identidad en \.
Ver [5] y [6].
Ejemplo. Sea un vector jo y sea 1 : R
n
R
n
la traslacin por , esto es,
1(A) = A +.
Entonces 1 es invertible con inversa G(1 ) = 1 .
Ejemplo. Sea l = (r, 0) [ r 0, 0 < 0 < . Sea
1(r, 0) = (r, j) = (r cos 0, r :c: 0).
La imagen de l es el medio plano superior
H = (r, j) [ j 0.
De las ecuaciones r = r cos 0, j = r :c: 0 podemos encontrar las funciones
componentes de la inversa G:
r =
_
r
2
+j
2
, 0 = cos
1
(r,r) ,
de manera que
1
1
(r, j) =
_
_
r
2
+j
2
, cos
1
(r,r)
_
.
Puede suceder que una funcin no sea invertible en todo su dominio aunque s
lo sea localmente alrededor de un punto 1 de su dominio l. Se dice que
1 : l R
n
R
n
es localmente invertible en 1 si existe un conjunto abierto
l
1
l conteniendo 1 de tal manera que 1 sea invertible en l
1
.
37
Ejemplo. Si vemos a la funcin 1 (r, 0) = (r cos 0, r :c: 0) del ejemplo
anterior como una funcin del plano R
2
en s mismo, entonces 1 no es
invertible en todo R
2
, sin embargo, es localmente invertible alrededor de todo
punto distinto del origen.
En muchos casos puede resultar imposible encontrar explcitamente las
frmulas que denen a la funcin inversa, aunque existe una manera de saber
si existe una inversa local, como se enuncia a continuacin.
Teorema de la Funcin Inversa. Sea 1 : l R
n
R
n
una funcin de
clase C
1
. Si el determinante Jacobiano de 1 en un punto 1 l es distinto de
cero, entonces 1 es localmente invertible en 1.
La prueba se da en cursos ms avanzados de clculo. Ver, por ejemplo, [6].
Aqu solamente haremos algunas observaciones y veremos algunos ejemplos.
Del lgebra lineal se sabe que si el determinante de una matriz cuadrada es
distinto de cero, entonces la matriz es invertible. En consecuencia, si el
determinante Jacobiano no se anula en 1, resulta invertible la matriz
Jacobiana, esto es, la derivada es invertible. Podemos entonces reformular el
Teorema de la Funcin Inversa diciendo que si la derivada 11(1) es invertible
en un punto 1, entonces 1 es localmente invertible en 1. Normalmente es
muy fcil determinar cundo se anula un determinante, luego el Teorema de la
Funcin Inversa nos da un criterio simple para la invertibilidad local.
An cuando sea imposible encontrar explcitamente la funcin inversa 1
1
siempre se puede hallar la derivada de 1
1
, si existe, por una sencilla frmula.
Supongamos que 1 : l R
n
\ R
n
tiene una inversa G : \ l.
Entonces G 1 = 1, la identidad en l. Como la derivada de la identidad es la
identidad, la regla de la cadena nos permite escribir lo siguiente:
1G(1(A)) 11(A) = 1
para toda A l. Sea 1 = 1(A) y multipliquemos ambos lados de la ecuacin
anterior por la matriz inversa de la derivada de 1 en A para obtener que
1(1
1
)(1 ) = (11(A))
1
,
esto es, la derivada de la inversa es la inversa de la derivada.
Ejemplo. Sea 1(r, j) = (c
r
cos j, c
r
:c: j). La matriz Jacobiana es
J
J
(r, j) =
_
c
r
cos j c
r
:c: j
c
r
:c: j c
r
cos j
_
,
con determinante
det J
J
(r, j) = c
r
,= 0
38
para toda r, luego 1 es localmente invertible en (r, j) para toda r, j.
Ejemplo. Sea l R
2
abierto y sea ) : l R de clase C
1
. Sea (a, /) l y
supongamos que
0)
0j
(a, /) ,= 0. Sea 1 : l R
2
R
2
denida por
1(r, j) = (r, )(r, j)).
Se tiene que
J
J
(r, j) =
_
_
1 0
0)
0r
0)
0j
_
_
,
luego la matriz jacobiana
J
J
(a, /) =
_
_
1 0
0)
0r
(a, /)
0)
0j
(a, /)
_
_
tiene determinante
det J
J
(a, /) =
0)
0j
(a, /) ,= 0.
Entonces, el Teorema de la Funcin Inversa nos garantiza que 1(r, j) es
localmente invertible en (a, /).
Vamos a usar el resultado del ejemplo anterior para estudiar las funciones
implcitas.
Sea ) : l R
2
R de clase C
1
en un abierto l con )(a, /) = c. Nos
preguntamos por la existencia de una funcin diferenciable j = ,(r) denida
alrededor de r = a de modo que ,(a) = / y )(r, ,(r)) = c para toda r
sucientemente cerca de a. Si tal funcin existe, decimos que j = ,(r) est
determinada implcitamente por ) (r, j).
Teorema de la Funcin Implcita. Sean l R
2
abierto y ) : l R de
clase C
1
en l. Sea (a, /) l y supongamos que
0)
0j
(a, /) ,= 0 con )(a, /) = c.
Entonces existe una funcin implcita j = ,(r) de clase C
1
en algn intervalo
abierto conteniendo a tal que ,(a) = / y )(r, ,(r)) = c.
Demostracin. Por un ejemplo anterior ya sabemos que
1(r, j) = (r, )(r, j)) es localmente invertible en (a, /). Obsrvese que
1(a, /) = (a, c). Si la funcin inversa de 1 se escribe como
G(n, ) = (r, j),
39
tenemos que
1(r, j) = (n, ) = (r, )(r, j)) ,
de donde
n = r,
= )(r, j),
son las ecuaciones que denen a 1. Como ya sabemos que existe la inversa de
1, estas ecuaciones pueden invertirse, dando lugar a las ecuaciones que denen
a la inversa local G, las cuales podemos escribir as:
r = n,
j = q(n, ),
para alguna funcin q de clase C
1
, obteniendo G(n, ) = (n, q(n, )) en algn
abierto del plano.
Si denimos ,(r) = q(r, c) tenemos, por un lado que
1(r, ,(r)) = 1(r, q(r, c)) = 1(G(r, c)) = (r, c),
mientras que, por otro lado,
1(r, ,(r)) = (r, )(r, ,(r))).
En consecuencia,
)(r, ,(r)) = c
donde , es de clase C
1
en algn intervalo abierto alrededor de a. Adems,
como G(a, c) = 1
1
(a, c) = (a, /), tenemos que q(a, c) = / = ,(a).
Ejemplo. Sea )(r, j) = r
2
+j
2
y sea (a, /) = (1, 1). Entonces
c = )(1, 1) = 2. Tenemos
0)
0j
(r, j) = 2j, por tanto
0)
0j
(1, 1) = 2 ,= 0. Por el
Teorema de la Funcin Implcita, existe j = ,(r) denida implcitamente
alrededor de r = 1. Aqu podemos, adems, resolver explcitamente para
encontrar
j =
_
2 r
2
.
Ejemplo. Sea )(r, j) = r
2
j + 3j
3
r
4
4. Tomemos (a, /) = (1, 1) de modo
que )(a, /) = 0. Entonces
0)
0j
(r, j) = r
2
+ 9j
2
r
4
, y resulta
0)
0j
(1, 1) = 10 ,= 0,
40
luego existe una funcin implcita j = ,(r), aunque no hay un modo fcil de
hallarla. Sin embargo, derivando la ecuacin )(r, j) = 0 sabiendo que j es
una funcin diferenciable de r, encontramos que
2rj +r
2
j
0
+ 12j
3
r
3
+ 9j
2
j
0
r
4
= 0,
de donde podemos despejar la derivada j
0
para obtener
,
0
(r) = j
0
=
2rj + 12j
3
r
3
r
2
+ 9j
2
r
4
.
Entonces, por ejemplo el valor de la derivada se puede hallar en cualquier
punto, an sin conocer la funcin explcita. Por ejemplo,
,
0
(1) =
7
5
.
1.3.8. Divergencia y Rotacional.
Ahora veremos dos operaciones bsicas que se pueden hacer con un campo
vectorial 1 = 1
1
i +1
2
j +1
3
k. Una es la divergencia, denida como sigue:
div 1 =
01
1
0r
+
01
2
0j
+
01
3
0.
.
Una notacin muy usada en las aplicaciones a las ciencias fsicas es la
siguiente. Si denotamos por \ (lase nabla) al operador
\ = i
0
0r
+j
0
0j
+k
0
0.
,
entonces la divergencia se puede denotar por \ 1, como si fuera un producto
punto. Una de las interpretaciones fsicas de la divergencia de un campo
vectorial tiene que ver con la razn a la cual se est expandiendo el ujo
determinado por el campo. Por ejemplo, si 1(r, j, .) = ri +jj +.k representa
el campo de velocidad de un uido, entonces div 1 = 3, lo cual signica que el
uido se expande a una razn de 3 unidades cbicas por unidad de volumen,
por unidad de tiempo.
El otro producto que se puede obtener entre el operador \ y un campo
vectorial 1 = 1
1
i +1
2
j +1
3
k es el rotacional, denido por
rot 1 =
_
01
3
0j

01
2
0.
_
i +
_
01
1
0.

01
3
0r
_
j +
_
01
2
0r

01
1
0j
_
k,
41
el cual se puede recordar ms fcilmente si lo escribimos usando al operador \
como si se hiciera el producto cruz con el campo:
rot 1 = \1 =

i j k
0
0r
0
0j
0
0.
1
1
1
2
1
3

.
Ejemplo. Sea 1(r, j, .) = ri +rjj +k. Entonces
\1 =

i j k
0
0r
0
0j
0
0.
r rj 1

= jk.
Existen muchas propiedades que cumplen estas operaciones. Una de ellas la
probamos a continuacin.
Teorema. Para toda funcin )(r, j, .) real-valuada de clase C
2
se cumple que
\(\)) = 0,
esto es, el rotacional de un gradiente es cero.
Demostracin. Es un clculo directo:
\(\)) =

i j k
0
0r
0
0j
0
0.
0)
0r
0)
0j
0)
0.

=
_
0
2
)
0j 0.

0
2
)
0. 0j
_
i +
_
0
2
)
0. 0r

0
2
)
0r 0.
_
j +
_
0
2
)
0r 0j

0
2
)
0j 0r
_
k,
lo cual se anula debido a la igualdad entre todas las derivadas parciales mixtas
de segundo orden para una funcin )(r, j, .) de clase C
2
.
Otra propiedades bsicas se enlistan a continuacin, donde las letras
minsculas ), q denotan campos escalares y las maysculas 1, G denotan
campos vectoriales.
42
1. \() +q) = \) +\q
2. \(c)) = c\), para una constante c
3. \()q) = )\q +q\)
4. \(),q) = (q\) )\q) ,q
2
, donde no se anule q
5. \ (1 +G) = \ 1 +\ G
6. \(1 +G) = \1 +\G
7. \ ()1) = )(\ 1) +1 (\))
8. \ (1 G) = G(\1) 1 (\G)
9. \ (\1) = 0
10. \()1) = )(\1) + (\)) 1
Ejemplo. Sea r = ri +jj +.k. Si denotamos por r a |r|, encontremos \r y
\ (rr).
Se tiene que
\r =
_
0r
0r
,
0r
0j
,
0r
0.
_
.
Ahora, como r = |r| =
_
r
2
+j
2
+.
2
, resulta que para r ,= 0,
0r
0r
=
r
_
r
2
+j
2
+.
2
=
r
r
.
Entonces
\r =
_
r
r
,
j
r
,
.
r
_
=
r
r
.
Para encontrar \ (rr) usamos la frmula 7 de arriba para escribir
\ (rr) = r (\ r) +r (\r),
donde \ r =
0r
0r
+
0j
0j
+
0.
0.
= 3. Luego
\ (rr) = 3r +r
r
r
= 3r +
|r|
2
r
= 3r +
r
2
r
= 4r.
43
En [1] y [3] se pueden ver diversas aplicaciones de los conceptos anteriores a
las ciencias fsicas.
1.4. Ejercicios y problemas.
1. Usando la denicin de diferenciabilidad, justica que si ) : l R
n
R
es diferenciable en x
o
l, entonces
) (x
0
+h) ) (x
0
) = \)(x
0
) h +q(h),
donde
lim
h!0
q(h)
|h|
= 0.
2. Sea ) : R
2
R denida por
)(r, j) =
_

_
0 :i (r, j) = (0, 0)
r
3
r
2
+j
2
:i (r, j) ,= (0, 0)
(a) Calcular las derivadas parciales de ) en el origen, esto es,
0)
0r
(0, 0) ,
0)
0j
(0, 0)
(b) Comprueba que la derivada parcial de ) respecto a r es la siguiente
funcin:
0)
0r
(r, j) =
_

_
1 :i (r, j) = (0, 0)
r
4
+ 3r
2
j
2
(r
2
+j
2
)
2
:i (r, j) ,= (0, 0)
(c) Es continua la funcin
J}
Jr
: R
2
R en el origen?
3. Para la curva q (t) = (c
|
, cos t, :c: t) y para la funcin
) (r, j, .) = r. +j. +rj
encontrar la siguiente derivada:
d
dt
() q) (t) [
|=1
44
4. Sea ) : R
2
R denida por
)(r, j) =
_

_
0 :i (r, j) = (0, 0)
2rj
2
r
2
+j
4
:i (r, j) ,= (0, 0)
(a) Verica que existen las derivadas parciales 0),0r, 0),0j en todos los
puntos (r, j) R
2
.
(a) Demuestra que existe la derivada direccional de ) en cualquier punto (r, j)
y en cualquier direccin determinada por un vector unitario u R
2
.
(c) Muestra que ) no es continua en el origen.
5. Sea ) : R
2
R denida por
)(r, j) =
_

_
0 :i (r, j) = (0, 0)
rj
r
2
j
2
r
2
+j
2
:i (r, j) ,= (0, 0)
(a) Comprueba que
0)
0j
(r, 0) = r para toda r.
(b) Comprueba que
0)
0r
(0, j) = j para toda j.
(c) Verica que
0
2
)
0r0j
(0, 0) ,=
0
2
)
0j0r
(0, 0).
45
2. Integracin en dos y tres
variables.
En la teora de integracin de funciones de una variable real se pueden
construir pruebas sencillas de la existencia de la integral de una funcin
continua denida sobre un intervalo usando sumas de Riemann. Para
funciones de varias variables se necesitan algunas tcnicas ms sosticadas de
las que disponemos para poder desarrollar pruebas completas de los teoremas.
Por tal razn omitiremos algunas de las demostraciones en esta unidad,
excepto en casos especiales donde las pruebas resulten comprensibles para el
nivel de este curso. Las pruebas rigurosas pertenecen a cursos avanzados de
clculo y de anlisis matemtico. Sin embargo justicaremos las pruebas
omitidas con argumentos geomtricos cuando sea posible.
2.1. Integral de Riemann.
2.1.1. Deniciones bsicas.
Comencemos por analizar los anlogos de las sumas superiores e inferiores
asociadas con particiones del dominio de integracin.
Sea 1 un rectngulo cerrado de : dimensiones y sea ) : 1 R
n
R una
funcin acotada, esto es,
[)(r, j)[ _ '
para todo punto (r, j) 1.
Una particin 1 de un intervalo cerrado [a, /] es una sucesin t
o
, . . . , t
|
,
donde
a = t
0
_ t
1
_ _ t
|
= /.
La particin 1 divide el intervalo [a, /] en / subintervalos [t
I1
, t
I
]. Una
particin del rectngulo :-dimensional [a
1
, /
1
] [a
n
, /
n
] es una coleccin
1 = (1
1
, . . . , 1
n
) ,
donde cada 1
I
es una particin del intervalo [a
I
, /
I
]. Supngase, por ejemplo,
que 1
1
= t
o
, . . . , t
|
es una particin de [a
1
, /
1
] y 1
2
= :
o
, . . . , :
l
es una
particin de [a
2
, /
2
]. Entonces la particin 1 = (1
1
, 1
2
) de [a
1
, /
1
] [a
2
, /
2
]
lo divide en / | subrectngulos, cada uno de la forma [t
I1
, t
I
] [:
1
, :

].
En general, si 1
I
divide [a
I
, /
I
] en
I
subintervalos, entonces 1 = (1
1
, . . . , 1
n
)
divide [a
1
, /
1
] [a
n
, /
n
] en =
1

n
subrectngulos, los cuales
son llamados subrectngulos de la particin 1.
Ver [4] y [6].
46
Para un rectngulo :-dimensional, una funcin acotada ) : 1 R
n
R, una
particin 1 de 1 y un subrectngulo o de la particin 1, se dene:
:
S
()) = inf )(r) [ r o ,
'
S
()) = sup)(r) [ r o .
Ahora, el volumen \ (o) de o = [a
1
, /
1
] [a
n
, /
n
] se dene por el
producto
(/
1
a
1
) (/
n
a
n
)
y tambin es el volumen del conjunto (a
1
, /
1
) (a
n
, /
n
).
La suma inferior de ) respecto a 1 se dene por:
1(), 1) =

S
:
S
()) \ (o),
y la suma superior es:
l(), 1) =

S
'
S
()) \ (o).
Es claro que 1(), 1) _ l(), 1).
Lema. Supngase que la particin 1
0
es ms na que la particin 1 (lo cual
signica que cada subrectngulo de 1
0
est contenido en un subrectngulo de
1). Entonces:
1(), 1) _ 1(), 1
0
), j l(), 1
0
) _ l(), 1).
Demostracin. Cada subrectngulo o de 1 se divide en varios
subrectngulos o
1
, . . . , o
o
de 1
0
, de manera que
\ (o) = \ (o
1
) + +\ (o
o
).
Ahora, :
S
()) _ :
Si
()), ya que los valores )(r) para r o incluyen todos los
valores )(r) para r o
I
y posiblemente otros ms pequeos. As,
:
S
()) \ (o) = :
S
()) \ (o
1
) + +:
S
()) \ (o
o
)
_ :
S1
()) \ (o
1
) + +:
S
()) \ (o
o
).
La suma, para todo o, de los trminos del lado izquierdo es 1(), 1), mientras
que la suma de todos los trminos del lado derecho es 1(), 1
0
). Por lo tanto
1(), 1) _ 1(), 1
0
). La otra desigualdad se demuestra de manera similar.
Corolario. Si 1 y 1
0
son dos particiones cualesquiera, entonces
1(), 1
0
) _ l(), 1).
47
Demostracin. Sea 1
00
una particin ms na que ambas 1 y 1
0
. Por
ejemplo, sea 1
00
= (1
00
1
, . . . , 1
00
n
) , donde 1
00
I
es una particin de [a
I
, /
I
] ms
na que ambas 1
I
y 1
0
I
. Entonces
1(), 1
0
) _ 1(), 1
00
) _ l(), 1
00
) _ l(), 1).
De este corolario se deduce que la mnima cota superior de todas las sumas
inferiores de ) es menor o igual que la mxima cota inferior de todas las sumas
superiores de ).
Denicin. Una funcin ) : 1 R se dice integrable en el rectngulo 1 si
) es acotada y se cumple la siguiente igualdad:
sup1(), 1) = inf l(), 1) .
En caso de que ) sea integrable, el nmero que cumple la igualdad anterior se
denota por:
_
1
)
y es llamado la integral de ) sobre 1. Ver [3], [4] y[6].
Con mucha frecuencia se denota la integral de ) sobre 1 por:
_
1
) (r
1
, . . . , r
n
) dr
1
dr
n
,
y si ) : [a, /] R, tambin suele escribirse
_
b
o
) =
_
[o,b]
).
2.2. Existencia de la Integral.
2.2.1. Integrabilidad.
Un criterio simple y til de integrabilidad se enuncia y prueba a continuacin.
Teorema. Una funcin acotada ) : 1 R
n
R es integrable si y slo si
\- 0 existe una particin 1 de 1 tal que
l(), 1) 1(), 1) < -.
48
Antes de ver la demostracin, obsrvese que una funcin continua denida en
un compacto resulta integrable por el teorema anterior.
Demostracin. Si se cumple la condicin, resulta que
sup1(), 1) = inf l(), 1)
y de ah que ) sea integrable. Por otro lado, si ) es integrable, de modo que
sup1(), 1) = inf l(), 1) ,
entonces para cualquier - 0 existen particiones 1 y 1
0
que satisfacen
l(), 1) 1(), 1
0
) < -.
Si 1
00
es ms naque ambas 1 y 1
0
, un lema previo implica que
l(), 1
00
) 1(), 1
00
) _ l(), 1) 1(), 1
0
) < -.
En lo que sigue vamos a caracterizar las funciones integrables y veremos un
mtodo para calcular integrales. Por ahora consideremos dos ejemplos de
funciones, siendo una integrable y la otra no.
Ejemplo. Sea ) : 1 R
n
R una funcin constante, ) (r) = c. Entonces
para cualquier particin 1 y cualquier subrectngulo o, se tiene que
:
S
()) = '
S
()) = c,
por lo tanto
1(), 1) = l(), 1) =

S
c \ (o) = c \ (1),
luego
_
1
) = c \ (1).
Ejemplo. Sea ) : 1 R
n
R denida por
)(r) =
_
0 si r es racional,
1 si r es irracional.
Si 1 es una particin, entonces todo subrectngulo o contiene puntos (r, j)
con r racional, y tambin contiene puntos con r irracional. De ah que
:
S
()) = 0 y '
S
()) = 1, por lo tanto
1(), 1) =

S
0 \ (o) = 0
49
y adems
l(), 1) =

S
1 \ (o) = \ ([0, 1] [0, 1]) = 1.
En consecuencia, ) no es integrable.
2.2.2. Medida cero y contenido cero.
Un subconjunto de R
n
tiene medida cero (:-dimensional), si para cada
- 0 existe una cubierta de por rectngulos cerrados l
1
, l
2
, l
3
, . . . tales
que
1

I=1
\ (l
I
) < -.
Ver [1], [4], [6]
Es claro que si tiene medida cero y 1 , entonces 1 tiene medida cero.
Observaciones:
1. Pueden usarse rectngulos abiertos en lugar de rectngulos cerrados en las
deniciones anteriores.
2. Un conjunto que tiene solamente un nmero nto de puntos tiene medida
cero.
3. Si tiene innitos puntos que pueden ponerse en una sucesin a
1
, a
2
, a
3
, . . . ,
entonces tiene medida cero.
Las pruebas de las observaciones 1 y 2 son inmediatas. Para demostrar la
tercera tomemos cualquier - 0. Se puede elegir un rectngulo cerrado l
I
conteniendo a
I
de manera que
\ (l
I
) < -,2
I
.
Entonces
1

I=1
\ (l
I
) <
1

I=1
-,2
I
= -.
Otro criterio de gran utilidad es el siguiente.
Teorema. Si =
1
'
2
'
3
' , y cada
I
tiene medida cero, entonces
tiene medida cero.
50
Demostracin. Sea - 0 arbitrario. Como
I
tiene medida cero, existe una
cubierta l
I1
, l
I2
, l
I3
, . . . de
I
por rectngulos cerrados tales que
1

=1
\ (l
I
) < -,2
I
.
Entonces la coleccin de todos los l
I
constituyen una cubierta de .
Consideremos ahora el siguiente arreglo:

l
11
l
12
l
13


l
21
l
22
l
23


l
31
l
32
l
33

Obsrvese que esta coleccin puede colocarse en una sucesin

\
1
, \
2
, \
3
, . . .
y que se cumple lo siguiente:
1

I=1
\ (\
I
) <
1

I=1
-,2
I
= -.
Denicin. Un subconjunto R
n
tiene contenido cero (:-dimensional)
si para todo - 0 existe una cubierta nita l
1
, l
2
, l
3
, . . . de por
rectngulos cerrados tales que
1

I=1
\ (l
I
) < -.
Ver [6].
Si tiene contenido cero, tiene claramente medida cero. De nuevo, pueden
considerarse rectngulos abiertos en lugar de rectngulos cerrados en la
denicin anterior.
2.2.3. Criterio de integrabilidad para funciones
discontinuas.
Si ) : R
n
R es acotada y c 0 usaremos los siguientes nmeros en lo
que sigue:
' (a, ), c) = sup)(r) [ r & [r a[ < c ,
:(a, ), c) = inf )(r) [ r & [r a[ < c .
51
Denicin. La oscilacin de una funcin ) en un punto a se dene por:
o (), a) = lim
o!0
[' (a, ), c) :(a, ), c)] .
Ver [6].
Este lmite siempre existe puesto que la diferencia
' (a, ), c) :(a, ), c)
decrece si c decrece.
Existen dos hechos importantes acerca de la oscilacin, que veremos enseguida.
Demostramos el primero y dejamos la prueba del segundo como ejercicio para
el lector.
Teorema. Una funcin acotada ) es continua en a == o(), a) = 0.
Demostracin. Sea ) continua en a. Para todo - 0 podemos elegir c 0
de manera que
[)(r) )(a)[ < -
para toda r con [r a[ < c.
As,
' (a, ), c) :(a, ), c) _ 2-.
Como lo anterior es vlido para toda - 0, se concluye que o(), a) = 0.
El regreso es similar.
Teorema. Sea R
n
cerrado. Si ) : R es cualquier funcin acotada y
- 0, entonces el conjunto
r [ o(), a) _ -
es acotado.
A continuacin se enuncia un criterio para decidir cundo es integrable una
funcin discontinua. La prueba es muy tcnica para el nivel de este curso por
lo cual no la presentamos aqu. El lector interesado puede ver una
demostracin en [6].
Teorema. Sean R
n
un rectngulo cerrado, ) : R acotada y
1 = r [ ) es discontinua en r .
52
Entonces ) es integrable == 1 tiene medida cero.
2.3. Propiedades bsicas de la Integral.
2.3.1. Linealidad y aditividad.
Teorema. Supngase que ), q son funciones denidas sobre un rectngulo 1,
y que son integrables sobre 1. Entonces ) +q es integrable. Si ` R,
entonces `) es integrable. Adems se cumple lo siguiente:
_
1
() +q) =
_
1
) +
_
1
q,
_
1
(`)) = `
_
1
).
En otros trminos, la integral es un operador lineal sobre el espacio vectorial
de las funciones integrables.
La demostracin depende de propiedades elementales de nmos y supremos y
se dejan para el lector interesado (ver [2]).
La propiedad de aditividad de la integral es la que se enuncia a continuacin.
Teorema. Sea una regin acotada del plano R
2
que puede expresarse como
unin de dos regiones
1
,
2
sin puntos en comn excepto posiblemente en
puntos frontera. Supngase que las fronteras de ,
1
,
2
son curvas
diferenciables. Si ) es una funcin denida en y es continua excepto en un
nmero nito de curvas diferenciables, entonces
_
.
) =
_
.1
) +
_
.2
).
La idea de la prueba es intuitivamente clara debido a que el rea de cualquier
curva es igual a cero.
2.3.2. Teorema del Valor Medio.
Los diversos teoremas del valor medio para integrales dan estimaciones del
clculo de integrales denidas usando ciertos valores de la funcin integrando.
Teorema. Si ) : [a, /] R es continua, existe un punto c (a, /) tal que
_
b
o
)(r) dr = (/ a))(c).
53
Demostracin. Defnase 1(r) =
_
r
o
)(t) dt y aplquese el teorema del valor
medio para derivadas a esta funcin 1.
Teorema. Supngase que ), q : [a, /] R son continuas y que q es no
negativa (o bien, no positiva).Entonces existe un punto c (a, /) tal que
_
b
o
)(r) q(r) dr = )(c)
_
b
o
q(r) dr.
Obsrvese que cuando q(r) = 1 para toda r [a, /], este segundo teorema se
reduce al primero.
Demostracin. Consideraremos el caso cuando q es no negativa. El otro caso
se deduce de lo anterior al reemplazar q por q. Sean
: = min)(r) [ r [a, /] ,
' = max )(r) [ r [a, /] .
Para toda r [a, /] se cumple que
:q(r) _ )(r)q(r) _ 'q(r).
Ahora, por denicin de integral denida, tenemos que si 1 : [a, /] R es
continua y 1(r) _ 0 siempre, entonces
_
b
o
1(r) dr _ 0,
de donde se deduce que si G, H : [a, /] R son funciones continuas y
G(r) _ H(r) para toda r [a, /], entonces
_
b
o
G(r) dr _
_
b
o
H(r) dr.
Integrando las primeras desigualdades sobre [a, /] y usando la ltima se
obtiene que
:
_
b
o
q(r) dr _
_
b
o
)(r)q(r) dr _ '
_
b
o
q(r) dr.
Por simplicidad, denotemos
1 =
_
b
o
q(r) dr.
Como q(r) _ 0 para toda r [a, /], la desigualdad
_
b
o
1(r) dr _ 0 implica
que 1 _ 0. Si 1 = 0, entonces las ltimas desigualdades nos permiten escribir
que los dos lados de la igualdad
_
b
o
)(r) q(r) dr = )(c)
_
b
o
q(r) dr
54
son cero, estableciendo su validez para cualquier c. Finalmente, si 1 0,
dividimos
:
_
b
o
q(r) dr _
_
b
o
)(r)q(r) dr _ '
_
b
o
q(r) dr
entre 1 para obtener que
: _
1
1
_
b
o
)(r)q(r) dr _ '.
La continuidad de ) en el cerrado [a, /] garantiza la existencia de sus valores
mnimo y mximo, lo cual implica la igualdad postulada para alguna
c (a, /).
Para integrales sobre regiones bidimensionales el resultado anlogo al primer
teorema es el siguiente.
Teorema. Supongamos que ) : 1 R
2
R es continua y 1 es una regin
con rea (1). Entonces existe un punto (r
o
, j
o
) 1 tal que
__
1
)(r, j) dr dj = )(r
o,
j
o
)(1).
La idea de la demostracin es similar a las anteriores y se deja como ejercicio
al lector (ver [1]).
2.4. El Teorema de Fubini.
El problema de calcular integrales se resuelve, en principio, por el teorema de
Fubini que reduce el clculo de integrales sobre rectngulos en R
n
, para : 1,
al clculo de integrales sobre intervalos cerrados de nmeros reales. La idea del
teorema para una funcin continua positiva ) : [a, /] [c, d] R es la
siguiente. Sea
t
0
, . . . , t
n
una particin de [a, /] y divdase el producto cartesiano [a, /] [c, d] en :
bandas de la forma
t
I
[c, d] .
Si q
r
se dene por q
r
(j) = )(r, j), entonces el rea de la regin bajo la grca
de ) y encima de r [c, d] es
_
J
c
q
r
=
_
J
c
)(r, j) dj.
55
El volumen de la regin bajo la grca de ) encima de
[t
I1
, t
I
] [c, d]
es aproximadamente igual a
(t
I
t
I1
)
_
J
c
)(r, j) dj,
para cada r [t
I1
, t
I
]. As,
_
[o, b][c, J]
) =
n

I=1
_
[|i1, |i][c, J]
)
es aproximadamente igual a
n

I=1
(t
I
t
I1
)
_
J
c
)(r
I
, j) dj,
con r
I
[t
I1
, t
I
].
Por otro lado, aparecen sumas similares en la denicin de la integral
_
b
o
_
_
J
c
)(r, j) dj
_
dr.
Luego, si / se dene por
/(r) =
_
J
c
q
r
=
_
J
c
)(r, j) dj,
resulta razonable esperar que / sea integrable en [a, /] y que
_
[o, b][c, J]
) =
_
b
o
/ =
_
b
o
_
_
J
c
)(r, j) dj
_
dr
cuando ) es continua.
Hemos hecho intuitivamente claro el hecho enunciado a continuacin.
Teorema de Fubini. Sea ) una funcin continua denida sobre un
rectngulo 1 = [a, /] [c, d]. Entonces
_
b
o
_
_
J
c
)(r, j) dj
_
dr =
_
J
c
_
_
b
o
)(r, j) dj
_
dr.
El nmero denido por cada lado de la igualdad anterior se denota
frecuentemente por
__
1
)(r, j) dr dj,
56
o tambin por
_
b
o
_
J
c
)(r, j) dj dr
y por notaciones similares (ver [6]).
2.5. Integrales dobles y triples.
Ahora veremos ejemplos del clculo de integrales dobles mediante la aplicacin
del teorema de Fubini.
Ejemplo. Sea )(r, j) = r
2
j. Encontrar la integral doble de ) sobre el
rectngulo [1, 2] [3, 4].
Debemos calcular
_
2
1
_
4
3
)(r, j) dj dr.
Para esto, calculamos primero la integral respecto a j,
_
4
3
r
2
j dj.
Para un valor jo de r, ponemos r
2
fuera de la integral:
r
2
_
4
3
j dj = r
2
j
2
2

4
3
=
7r
2
2
.
Al integrar lo anterior respecto a r resulta nalmente
_
2
1
7r
2
2
dr =
49
6
.
2.5.1. Integracin sobre regiones elementales.
Sean q
1
, q
2
dos funciones en [a, /] tales que q
1
(r) _ q
2
(r). Sean c, d tales que
c < q
1
(r) _ q
2
(r) < d
para toda r [a, /]. Entonces estas funciones determinan una regin entre
las dos rectas
r = a, r = /,
y entre las dos curvas
j = q
1
(r), j = q
2
(r).
57
Esta regin es del tipo denominado regin elemental de tipo 1.
Si ) es una funcin continua en , y denimos ) en el rectngulo [a, /] [c, d]
igual a cero en cualquier punto del rectngulo que no intersecte , entonces
para toda r [a, /] la integral
_
J
c
)(r, j) dj
puede escribirse
_
1(r)
c
)(r, j) dj +
_
2(r)
1(r)
)(r, j) dj +
_
J
2(r)
)(r, j) dj.
Ahora, como ) (r, j) = 0 siempre que
c _ j < q
1
(r) j q
2
(r) < j _ d,
la primera integral y la ltima son iguales a cero. Por lo tanto
_
.
) =
_
b
o
_
2(r)
1(r)
)(r, j) dj dr.
Las regiones elementales de tipo 2 son de la forma
_
(r, j) R
2
[ c _ j _ d, /
1
(j) _ r _ /
2
(j)
_
,
y las integrales dobles denidas sobre ellas se pueden calcular de acuerdo a la
frmula
_
.
) =
_
J
c
_
|2()
|1()
)(r, j) dr dj,
similarmente al caso anterior.
Ver [1], [2], [3] y [4].
2.5.2. Cambio del orden de integracin.
Supongamos que es una regin que puede describirse como del tipo 1 y
tambin como del tipo 2. En tal caso se puede calcular la integral doble de una
funcin denida sobre con cualquiera de las dos frmulas de la seccin 2.5.1.
En consecuencia, si una de las dos integrales resulta muy complicada de
calcular se puede cambiar a la otra integral. Esta tcnica se llama cambio del
orden de integracin.
Ejemplo. Calcular
_
o
0
_
p
o
2
r
2
0
_
a
2
j
2
dj dr.
58
Obsrvese que r vara entre 0 y a, y que para cada r ja,
0 _ j _
_
a
2
r
2
.
As, la regin de integracin es el conjunto de puntos (r, j) tales que
0 _ r _ a, 0 _ j _
_
a
2
r
2
,
la cual es un cuarto del disco de radio a en el primer cuadrante. Por lo tanto
se puede describir tambin como el conjunto de puntos (r, j) que cumplen:
0 _ j _ a, 0 _ r _
_
a
2
j
2
.
De manera que
_
o
0
_
p
o
2
r
2
0
_
a
2
j
2
dj dr =
_
o
0
_
_
_
o
2

2
0
_
a
2
j
2
dr
_
dj
=
_
o
0
_
r
_
a
2
j
2
_
r=
_
o
2

2
r=0
dj
=
_
o
0
_
a
2
j
2
_
dj
=
_
a
2
j
j
3
3
_
o
0
=
2a
3
3
.
2.5.3. Integrales triples.
Todo lo dicho para integrales dobles puede generalizarse a tres dimensiones. Si
denota una regin tridimensional y ) es una funcin denida sobre , se
denota
_
.
) =
___
.
) (r, j, .) d. dj dr.
Para calcular integrales triples se tienen situaciones similares al caso
bidimensional. Si
1 = [a
1
, /
1
] [a
2
, /
2
] [a
3
, /
3
] ,
entonces
_
1
) =
_
b1
o1
_
_
b2
o2
_
_
b3
o3
) (r, j, .) d.
_
dj
_
dr.
59
Ejemplo. Calcular la integral de la funcin ) (r, j, .) = :c: r sobre el
rectngulo denido por
0 _ r _ , 2 _ j _ 3, 1 _ . _ 1.
La integral es igual a
_
t
0
_
3
2
_
1
1
:c: r d. dj dr.
Si primero integramos respecto a . obtenemos
.[
1
1
= 2.
A continuacin, con respecto a j, obtenemos
j[
3
2
= 1.
Finalmente,
_
t
0
2 :c: r dr = 2 cos r[
t
0
= 2 (cos cos 0) = 4.
Tambin existen integrales denidas sobre regiones ms generales que
rectngulos y que se describen con desigualdades.
Ejemplo. Considrese el tetrahedro T con vrtices en los puntos
(0, 0, 0) , (1, 0, 0), (0, 1, 0) , (0, 0, 1) .
La regin tridimensional acotada por T puede describirse por las siguientes
desigualdades:
0 _ r _ 1,
0 _ j _ 1 r,
0 _ . _ 1 r j.
Por lo tanto, si ) es una funcin denida sobre ,
_
.
) =
_
1
0
_
1r
0
_
1r
0
)(r, j, .) d. dj dr.
Para la funcin constante 1, esta integral nos da el volumen del tetrahedro, el
cual resulta ser igual a 1/6.
2.5.4. Teorema del Cambio de Variables.
60
Si q : [a, /] R es diferenciable con derivada continua y ) : R R es
continua, se sabe del clculo elemental que
_
(b)
(o)
) =
_
b
o
() q) q
0
cuya prueba es como sigue:
Si 1
0
= ), entonces (1 q)
0
= () q) q
0
, por tanto el lado izquierdo es
1 (q (/)) 1 (q (a)) ,
mientras que el lado derecho es
1 q(/) 1 q(a) = 1 (q (/)) 1 (q (a)) .
Se deja como ejercicio al lector demostrar que si q es inyectiva, entonces la
frmula anterior puede escribirse
_
((o,b))
) =
_
(o,b)
) q [q
0
[
La generalizacin de lo anterior a dimensiones superiores es el siguiente
resultado:
Teorema del Cambio de Variables. Sean R
n
abierto, q : R
n
inyectiva, diferenciable y con derivada continua tal que det q
0
(r) ,= 0 para toda
r . Si ) : q() R es integrable, entonces
_
(.)
) =
_
.
() q) [det q
0
[
La demostracin usa herramientas ms avanzadas de las que hasta ahora han
sido expuestas al estudiante normal de este curso, por lo que la omitimos. El
lector interesado puede consultarla en [6].
2.6. Ejercicios y problemas.
1. Calcular la integral doble
_
1
0
_
1
0
(rjc
r+
) dj dr.
2. Sea ) continua en el rectngulo 1 = [a, /] [c, d] y defnase
1(r, j) =
_
r
o
_

c
)(n, ) d dn.
61
Demostrar que
0
2
1
0r0j
=
0
2
1
0j0r
= )(r, j).
Utiliza este ejercicio para describir la relacin entre el teorema de Fubini y el
teorema siguiente: "Si 1(r, j) es de clase C
2
entonces son iguales las
derivadas parciales mixtas".
3. Utiliza el principio de Cavalieri para vericar que el volumen del slido
obtenido al hacer girar alrededor del eje x la grca de la parbola
j = r
2
+ 2r + 3
en el intervalo 1 _ r _ 3 es igual a
512
15
.
4. Usar integracin doble para encontrar el rea de una regin del plano
acotada por una elipse con semiejes de longitudes a, /.
5. Sea ) : R
2
R denida por )(r, j) = c
stn(r+)
y sea
1 = [, ] [, ]. Demuestra que se cumple lo siguiente:
1
c
_
1
4
2
__
1
)(r, j) dj dr _ c
6. Cambiar el orden de integracin en la siguiente integral doble:
_
1
0
_
1
r
rj dj dr
7. Calcular el volumen del slido acotado por el plano XZ, el plano YZ, el
plano XY, los planos r = 1, j = 1, y la supercie . = r
2
+j
4
.
8. Calcular la siguiente integral cambiando a coordenadas polares
_
o/
p
2
0
_
_
o
2

r dr dj.
9. Cmo podras justicar que
_
1
1
_
1
1
c
(r
2
+
2
)
dr dj = ?
62
10. Calcular el volumen de la regin acotada por el cilindro
r
2
+j
2
= 16,
por el plano . = 0, y que se encuentra debajo del plano
j = 2..
11. Usar integracin triple para encontrar el volumen de la regin del espacio
situada arriba del paraboloide
. = r
2
+j
2
y debajo de la esfera
r
2
+j
2
+.
2
= 1
12. Sea (n, ) = G(r, j) =
_
r +j, r
2
j
_
. Sea la regin del primer
cuadrante acotada por los ejes y por la lnea r +j = 2. Encontrar la integral
sobre G() de la funcin
) (n, ) =
1
_
1 + 4n + 4
13. Sea T : R
2
R
2
la transformacin lineal representada por la matriz
_
3 0
1 5
_
.
Si es el interior del crculo de radio 10, cul es el rea de la imagen de
bajo la transformacin lineal T?
14. Calcular el volumen acotado por el elipsoide
r
2
a
2
+
j
2
/
2
+
.
2
c
2
= 1
63
3. Integrales sobre Curvas y
Supercies.
3.1. Integrales de lnea.
3.1.1. Integral de lnea de campos escalares.
La integral de lnea de un campo escalar diferenciable ) (r, j, .) sobre una
curva diferenciable C : [a, /] R
3
tales que la composicin ) C (t) resulta
continua se dene por:
_
c
) d: =
_
b
o
) (C (t)) |C
0
(t)| dt.
Ver [1], [2], [3], [4], [5].
Ejemplo. Sean ) (r, j, .) = r
2
+j
2
+.
2
y
C(t) = (cos t, :c: t, t) , 0 _ t _ 2. Calcular la integral de lnea de ) sobre C.
Como
|C
0
(t)| =
_
:c:
2
t + cos
2
t + 1 =
_
2,
y
) (r(t), j(t), .(t)) = cos
2
t +:c:
2
t +t
2
= 1 +t
2
,
entonces
_
c
) d: =
_
2t
0
_
1 +t
2
_ _
2 dt =
_
2
_
t +
t
3
3
_
2t
0
=
2
_
2
3
_
3 + 4
2
_
.
3.1.2. Integral de lnea de campos vectoriales.
Sea 1 un campo vectorial continuo en R
3
denido sobre una curva
diferenciable C : [a, /] R
3
. Se dene la integral de lnea del campo 1 sobre
C por:
_
c
1 dr =
_
b
o
1 (C (t)) C
0
(t) dt.
64
Ver [1], [2], [3], [4], [5].
Ejemplo. Sean 1 (r, j, .) = (r, j, .) y C(t) = (:c: t, cos t, t) , 0 _ t _ 2.
Calcular la integral de lnea del campo 1 sobre C.
Tenemos la composicin
1 (C (t)) = (:c: t, cos t, t) ,
y
C
0
(t) = (cos t, :c: t, 1) .
Por lo tanto,
1(C(t)) C
0
(t) = :c: t cos t cos t :c: t +t = t,
y de ahi que
_
c
1 dr =
_
2t
0
t dt = 2
2
.
3.1.3. Teorema de Green.
Sean 1
1
, 1
2
dos funciones real-valuadas y diferenciables en una regin , que
es el interior de una curva C denida en el plano R
2
, diferenciable a trozos y
orientada positivamente. Entonces
_
c
1 dr =
__
.
_
01
2
0r

01
1
0j
_
dj dr,
donde 1 es el campo vectorial (1
1
, 1
2
) denido sobre la regin del plano
bidimensional Euclidiano.
Ver [1], [2], [3], [4], [5], [6].
Este teorema puede resultar til para cambiar el clculo de una integral de
lnea por el clculo de una integral doble que resulte ser ms fcil de realizar y
viceversa.
Ejemplo. Encontrar la integral del campo vectorial
1(r, j) = (j + 3r, 2j r)
sobre la elipse
4r
2
+j
2
= 4.
65
Sean 1
1
(r, j) = j + 3r, 1
2
(r, j) = 2j r. Entonces
01
2
0r
= 1,
01
1
0j
= 1.
Ahora, por el teorema de Green,
_
c
1 dr =
__
.
(2) dj dr = 2 rca(),
donde rca() es el rea de la elipse, que resulta ser a/, de donde obtenemos
nalmente que
_
c
1 dr = 2.
3.2. Integrales de supercie.
3.2.1. Supercies parametrizadas y orientadas.
Una supercie parametrizada o es un subconjunto del espacio tridimensional
que localmente (esto es, en una vecindad de cada uno de sus puntos) resulta
ser la imagen de una funcin A : 1 R
2
R
3
diferenciable sobre una regin
1 con matriz jacobiana de rango 2 y que tiene inversa continua. Esta funcin
A es llamada una parametrizacin de la supercie o.
Ejemplo. La esfera de radio j puede parametrizarse por
A (0, ,) = (j :c: , cos 0, j :c: , :c: 0, j cos ,) ,
donde
0 _ 0 _ 2, 0 _ , _
son los ngulos que denen la longitud y la latitud de cada punto de la esfera
de radio j con centro en el origen del espacio tridimensional R
3
.
Denicin. Una supercie se dice orientada si tiene un campo vectorial
diferenciable unitario que es perpendicular a su plano tangente en cada punto.
Ejemplo. La esfera parametrizada arriba es orientable con vector normal
unitario
=
A
0
A
,
|A
0
A
,
|
,
66
donde A
0
, A
,
son las derivadas parciales de la funcin A que parametriza la
esfera de arriba.
3.2.2. Integrales de supercie.
Sean 1 una regin del plano, A : 1 R
3
una parametrizacin de una
supercie o y ) : o R una funcin diferenciable denida sobre la supercie.
Se dene la integral de ) sobre o por
__
S
) do =
__
1
) (A (n, )) |A
u
A
u
| dn d.
Ver [1], [2], [3], [4], [5].
Ejemplo. Calcular la integral de )(r, j, .) = r sobre la supercie o denida
por
. = r
2
+j
sobre la regin 1 descrita por
0 _ r _ 1,
1 _ j _ 1.
Resulta que
__
S
r do =
__
1
r
_
1 +
_
0.
0r
_
2
+
_
0.
0j
_
2
dr dj
=
_
1
1
_
1
0
r
_
1 + 4r
2
+ 1 dr dj
=
1
8
_
1
1
_
1
0
_
2 + 4r
2
_
1/2
(8r) dr dj
=
2
3

1
8
_
1
1
_
_
2 + 4r
2
_
3/2
_
1
0
dj
=
1
12
_
1
1
_
6
3/2
2
3/2
_
dj
=
1
6
_
6
3/2
2
3/2
_
=
_
6
_
2
3
=
_
2
_
_
3
1
3
_
.
67
3.3. Ejercicios y problemas.
1. (a) Demostrar que la integral de lnea de una funcin escalar dada en
coordenadas cartesianas por ) (r, j) denida sobre una curva dada en
coordenadas polares por r = r(0), en un intervalo denido por 0
1
_ 0 _ 0
2
es
igual a:
_
02
01
) (r cos 0, r :c: 0)
_
r
2
+
_
dr
d0
_
2
d0.
(b) Calcular la longitud de arco de la curva r = 1 + cos 0, 0 _ 0 _ 2.
2. Encuentra el valor de la integral de lnea
_
c
j dr +
_
3j
3
r
_
dj +. d.
para C(t) =
_
t, t
2
, 0
_
, 0 _ t _ 1.
3. Usar el teorema de Green para calcular la integral de lnea
_
c
j
2
dr +r dj
para la trayectoria C denida por el permetro del cuadrado con vrtices en
(2, 0) , (0, 2), recorrido contrareloj.
4. Interpreta y demuestra la siguiente identidad:
_
J1
) \) n d: =
__
1
_
) \
2
) +\) \)
_
dr dj
5. Para la parametrizacin del paraboloide
A (n, 0) =
_
a ncos 0, a n :c: 0, n
2
_
,
con
0 < n < /, 0 < 0 < 2,
(a) encontrar los vectores tangentes
A
u
=
0A
0n
, A
0
=
0A
00
68
(b) calcular la norma del vector normal
=
0A
0n

0A
00
(c) obtener una ecuacin de la supercie en coordenadas cartesianas y
bosquejar su grca.
6. Demuestra que el rea de una supercie o denida por la grca de una
funcin . = )(r, j) de clase C
2
sobre una regin del plano 1 est dada por
rca(o) =
__
1
_
1 +
_
0)
0r
_
2
+
_
0)
0j
_
2
dr dj
7. Calcular el rea de la parte de la esfera
r
2
+j
2
+.
2
= 1
que queda dentro del cono
r
2
+j
2
= .
2
8. Calcular el rea de la supercie del toro generado al rotar alrededor del eje
. la circunferencia de radio r con centro en (0, a, 0) para a r.
9. Demostrar que si una supercie se dene implcitamente por una ecuacin
de la forma q (r, j, .) = 0,de manera que existe una funcin ) tal que
. = ) (r, j) est denida sobre una regin 1 del plano rj y satisface la
ecuacin q(r, j, )(r, j)) = 0, entonces el rea de dicha supercie est dada
por la siguiente integral:
__
1
_
q
2
r
+q
2

+q
2
:
[q
:
[
dr dj.
10. Encuentra el valor de la integral de supercie de la funcin dada sobre la
supercie indicada en cada inciso:
(a) ) (r, j, .) =
_
r
2
+j
2
_
.; sobre el hemisferio superior de una esfera de
radio 1 con centro en el origen.
(b) ) (r, j, .) = .; sobre la supercie dada por . = 1 r
2
j
2
para . _ 0.
(c) ) (r, j, .) = r
2
; sobre el cilindro r
2
+j
2
= 1 para 0 _ . _ 1.
69
11. Encuentra el valor de la integral de supercie del campo vectorial dado
sobre la supercie indicada en cada inciso:
(a) 1 (r, j, .) =
1
_
r
2
+
2
(j, j, 1); sobre el paraboloide
. = 1 r
2
j
2
, 0 _ . _ 1.
.
(b) 1 (r, j, .) = (j, r, 1); sobre la supercie parametrizada por
A(r; 0) = (r cos 0, r :c: 0, 0) , 0 _ r _ 1, 0 _ 0 _ 2
(c) 1 (r, j, .) = (r
2
, j
2
, .
2
); sobre la supercie parametrizada por
A(n; ) = (n +, n , n) , 0 _ n _ 2, 1 _ _ 3
70
Bibliografa
[1] Marsden, J. E., Tromba, A. J.; Clculo Vectorial ; Addison Wesley
Longman de Mxico, 4a. Edicin, 2001.
[2] Lang, S.; Calculus of several variables; Addison-Wesley, 1974.
[3] Apostol, T. M.; Calculus, Vol. 2; Revert; 1980.
[4] Courant, R., John, F.; Introduccin al clculo y al anlisis matemtico,
Vol. 2; Limusa; 1979.
[5] Pita Ruiz, C.; Clculo Vectorial ; Prentice-Hall Hispanoamericana;
1995.
[6] Spivak, M.; Calculus on Manifolds; W. A. Benjamin, Inc; 1965.
71