Professional Documents
Culture Documents
Review of Bas Stats For Econometric Success
Uploaded by
shaharhr1Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Review of Bas Stats For Econometric Success
Uploaded by
shaharhr1Copyright:
Available Formats
Econometrics
Review of Basic Statistics
Topics
1. Descriptive Statistics:
- 1 variable: Mean and Variance
- 2 variables: Covariance, Correlation
2. Hypothesis Testing
Descriptive Statistics
Inferential Statistics
Involves:
- Estimation
- Hypothesis Testing
Purpose:
- Make decisions about
population characteristics
Descriptive Statistics
Mean
Measure of central tendency
Affected by extreme values
Formula:
Median
Measure of central tendency
Middle value in ordered series
- If odd n, mean of the 2 middle values
Value that splits the distribution into two halves
Not affected by extreme values
Raw Data: 17 16 21 18 13 16 12 11
Ordered: 11 12 13 16 16 17 18 21
Position: 1 2 3 4 5 6 7 8
Mode
Measure of central tendency
Value that occurs most often
Not Affected by Extreme Values
There may be more than one mode
Raw Data: 17 16 21 18 13 16 12 11
Ordered: 11 12 13 16 16 17 18 21
Sample Variance
Measure of Dispersion around the Mean
Formula:
Sample Standard Deviation
Measure of Dispersion around the Mean
Has the same unit of measurement as the
variable itself
Formula:
Radom Variables
Random variable: numerical summary of a
random outcome
1. Discrete: only a discrete set of possible values
=> summarized by probability distribution: list of
all possible values of the variable and the
probability that each value will occur.
2. Continuous: continuum of possible values
=> summarized by the probability density
function (pdf)
Probability Distribution
1. List of pairs [ Xi, P(Xi) ]
Xi = Value of Random Variable (Outcome)
P(Xi) = Probability Associated with Value
2. 0 P(Xi) 1 - Mutually exclusive (no overlap)
3. P(Xi) = 1 - Collectively exhaustive (nothing
left out)
Mean and Variance: Discrete Case
Mean, or Expected Value
Weighted Average of All Possible Values
E(X) =
X
= XiP(Xi)
Variance
Weighted Average Squared Deviation about
the Mean
E(X) =
X
= (X
i
-
X
)
2
P(Xi)
Covariance
- measures joint variability of X and Y
For discrete RVs,
Can take any value in the real numbers
Depends on units of measurement (e.g., dollars, cents)
cov(X,Y) > 0 means that X and Y tend to move together
when y is above its mean, x tends to be above its mean
cov(X,Y) < 0 means that X and Y tend to move in opposite
directions
15
| | ) )( ( ) , cov(
Y X
Y X E Y X =
) , ( ) )( (
1
Y X P Y X
n
i
Y i X i
=
=
Correlation
A more convenient measure of the relationship between X
and Y is correlation since it is normalized to lie inside
[-1;1] interval.
-1 < corr(X,Y) < 1
If corr(X,Y) = 0, then X and Y are uncorrelated.
If corr(X,Y) > 0 , then X and Y are positively correlated.
If corr(X,Y) < 0, then X and Y are negatively correlated.
16
Y X
XY
Y X
Y X
Y X corr
o o
o
= =
) var( ) var(
) , cov(
) , (
Note
Covariance and correlation measure only linear
dependence!
Example: Cov(X,Y)=0
Does not necessarily imply that y and x are
independent.
They may be non-linearly related.
But if X and Y are jointly normally distributed,
then they are independent.
18
The correlation
coefficient
measures linear
association
The Mean and Variance of Sums of
Random Variables
19
) ( ) ( ) ( Y E X E Y X E + = +
) , cov( 2 ) var( ) var( ) var( Y X Y X Y X + + = +
) , cov( 2 ) var( ) var( ) var( Y X Y X Y X + =
Continuous Probability Distributions:
Normal Distribution
The notation reads X is Normally distributed
with mean and variance
2
The PDF for a normal RV is
The normal distribution has a familiar bell-shape.
The normal density is symmetric around its mean, and 95% of
probability density lies in the region .
20
) , ( ~
2
o N X
|
.
|
\
|
=
2
2
2
) (
2
1
exp
2
1
) (
o
to
x x f
) 96 . 1 , 96 . 1 ( o o +
o
=
X
Y
Effects of Varying Parameters
Infinite Number of Normal
Distribution Tables
Normal distributions differ by mean and
standard deviations
Each distribution would require its own table
Thats an infinite number of tables!
Standard Normal Distribution
If X is a Normal RV with mean and variance
2
has a normal distribution with mean 0
and variance 1, or standard normal distribution.
o
=
X
Z
Example
Values of the std normal CDF, ,
are tabulated in Appendix Table 1
To compute probabilities for a normal RV, it
must be standardized by subtracting its mean
and dividing by standard deviation
Example: Suppose Y ~ N(2,16), and we need
P(Y<0)
) ( ) ( z Z P z s = u
) 1 , 0 ( ~
4
2
N
Y
Z
=
3085 . 0 )
2
1
( )
4
2 0
( ) 0 ( = s =
s = s Z P Z P Y P
26
Moments: Skewness, Kurtosis
skewness =
( )
3
3
Y
Y
E Y
o
(
= measures asymmetry in a
distribution
- The larger the skewness (by absolute value), the more
asymmetric is distribution
- skewness = 0: distribution is symmetric
- skewness > (<) 0: distribution has long right (left) tail
kurtosis =
( )
4
4
Y
Y
E Y
o
(
- measure the thickness of tails
- kurtosis = 3: normal distribution
- kurtosis > 3: heavy tails (leptokurtotic), i.e. extreme events are
more likely to occur
27
Central Limit Theorem
Important Continuous Distributions
All derived from normal
distribution
2
distribution: arises from
sum of squared normal
random variables
t distribution: arises from
ratios of normal and
2
variables
F distribution: arises from
ratios of
2
variables.
Hypothesis Testing
Identifying Hypotheses
1. Formulate the question, e.g. test that the
population mean is equal to 3
2. State the question statistically (H
0
: = 3)
3. State its alternative statistically (H
1
: 3)
4. Choose level of significance
Typical values are 0.01, 0.05, 0.10
Rejection region of sampling distribution: the
unlikely values of sample statistic if null
hypothesis is true
Identifying Hypotheses: Examples
1. Is the population average amount of TV
viewing 12 hours?
H
0
: = 12
H
1
: 12
Choosing the Level of Significance:
Type I and Type II Errors
Type I Error: Reject a true null hypothesis.
Type II Error: Do not reject a false null.
We would like probabilities of both errors to be
small. BUT, we cannot make both very small at
the same time.
In statistics, we fix the probability of Type I error
at a significance level (e.g. 5%) and minimize the
probability of Type II error.
Hypothesis Testing: Basic Idea
Method 1: Compare Test Statistic to
Critical Value from the Table
1. Convert Sample Statistic (e.g., ) to standardized
Z variable
2. Compare to Critical Value from the table
If Z-test statistic falls in the rejection region,
reject H0;
Otherwise do not reject H0
Two-Sided Test: Rejection Regions
One-Sided Test: Rejection Region
Method 2: Compute the P-value
Probability of obtaining a test statistic more
extreme ( or ) than actual sample value given
H
0
is true.
The lowest significance level at which we reject H
0
Compute p-value for the test
Use this p-value to make rejection decision:
If p value , do not reject H
0
If p value < , reject H
0
P-values for 2-sided and 1-sided tests
Two-sided test: H
0
: =
0
H
1
:
0
One-sided test:
a. H
0
: >
0
b. H
0
: <
0
H
1
: <
0
H
1
: >
0
|
|
.
|
\
|
u =
|
|
.
|
\
|
> =
Y Y
Y Y
Z P value p
o
o
0 0
2 | |
|
|
.
|
\
|
u =
Y
Y
value p
o
0
1
|
|
.
|
\
|
u =
Y
Y
value p
o
0
P-value for a 2-Sided Test
Method 3: Confidence Intervals
Confidence interval: set of values that contains
the true population mean with a pre-specified
probability, say 95%.
This pre-specified probability is called confidence
level.
A 95% confidence interval for
Y
contains the true
value of
Y
in 95% of repeated samples.
The 90% CI is:
The 95% CI is:
The 99% CI is:
41
) ( 96 . 1 Y SE Y
) ( 58 . 2 Y SE Y
) ( 645 . 1 Y SE Y
Jarque-Bera Test for Normality
Assesses whether a given sample of data is
normally distributed
Aggregates information in the data about both
skewness and kurtosis
Test of the hypothesis that S = 0 and K = 3
The 5% critical value is 5.99; if JB > 5.99, reject
the null of normality.
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (894)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Employee Central Payroll PDFDocument4 pagesEmployee Central Payroll PDFMohamed ShanabNo ratings yet
- C79 Service Kit and Parts List GuideDocument32 pagesC79 Service Kit and Parts List Guiderobert100% (2)
- Bill of ConveyanceDocument3 pagesBill of Conveyance:Lawiy-Zodok:Shamu:-El80% (5)
- 04 Dasmarinas Vs Reyes GR No 108229Document2 pages04 Dasmarinas Vs Reyes GR No 108229Victoria Melissa Cortejos PulidoNo ratings yet
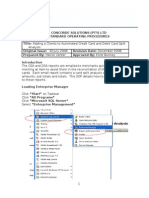
- SOP - Install ExactDocument5 pagesSOP - Install Exactshaharhr1No ratings yet
- 10 Reasons To Buy Pastel EvolutionDocument1 page10 Reasons To Buy Pastel Evolutionshaharhr1No ratings yet
- Edifact SampleDocument1 pageEdifact Sampleshaharhr1No ratings yet
- EFT SOP 19 December 2006Document20 pagesEFT SOP 19 December 2006shaharhr1No ratings yet
- Regression With Dummy Variables Econ420 1Document47 pagesRegression With Dummy Variables Econ420 1shaharhr1No ratings yet
- Call Centre Manual 04052007Document27 pagesCall Centre Manual 04052007shaharhr1No ratings yet
- Add merchants to credit card reportsDocument4 pagesAdd merchants to credit card reportsshaharhr1No ratings yet
- Upgrade Exact To A Newer VersionDocument2 pagesUpgrade Exact To A Newer Versionshaharhr1No ratings yet
- SOP - Checking Bank LinksDocument4 pagesSOP - Checking Bank Linksshaharhr1No ratings yet
- Self-Study Training Material & Assessment PricesDocument5 pagesSelf-Study Training Material & Assessment Pricesshaharhr1No ratings yet
- Recall A Tendered Order - Reprint A Receipt:: Kumnandi Food CompanyDocument5 pagesRecall A Tendered Order - Reprint A Receipt:: Kumnandi Food Companyshaharhr1No ratings yet
- Spectroscopy I (1a)Document6 pagesSpectroscopy I (1a)shaharhr1No ratings yet
- Here Are A Few Different Methods.: Method 1Document2 pagesHere Are A Few Different Methods.: Method 1shaharhr1No ratings yet
- Fastnet Radio Pad SetupDocument5 pagesFastnet Radio Pad Setupshaharhr1No ratings yet
- Principles of Accounting I: Jackson Community College ACCOUNTING 231-02 Winter 2013Document8 pagesPrinciples of Accounting I: Jackson Community College ACCOUNTING 231-02 Winter 2013shaharhr1No ratings yet
- Business Analytics For Pastel EvolutionDocument4 pagesBusiness Analytics For Pastel Evolutionshaharhr1No ratings yet
- HelloDocument1 pageHelloshaharhr1No ratings yet
- Spectroscopy I (1a)Document6 pagesSpectroscopy I (1a)shaharhr1No ratings yet
- Teaching Mark TwainDocument5 pagesTeaching Mark Twainshaharhr1No ratings yet
- Advertisements - The CBSE Way: Format and Marking SchemeDocument5 pagesAdvertisements - The CBSE Way: Format and Marking Schemeshaharhr1No ratings yet
- Evolution Manual - Fixed Assets PDFDocument44 pagesEvolution Manual - Fixed Assets PDFshaharhr1No ratings yet
- History of Electric VehiclesDocument8 pagesHistory of Electric Vehiclesshaharhr1No ratings yet
- CBSE Class 11 English Core Sample Paper-01Document7 pagesCBSE Class 11 English Core Sample Paper-01cbsesamplepaper80% (5)
- Maths Class 11Document7 pagesMaths Class 11shaharhr1No ratings yet
- Yahoo! Sports: Baseball Chicago CubsDocument3 pagesYahoo! Sports: Baseball Chicago Cubsshaharhr1No ratings yet
- Binder clientBasedLawyeringDocument9 pagesBinder clientBasedLawyeringshaharhr1No ratings yet
- ERISA Class Notes (Spring 2011) - 1Document107 pagesERISA Class Notes (Spring 2011) - 1shaharhr1100% (1)
- Barbri Corp OutlineDocument12 pagesBarbri Corp Outlineshaharhr1100% (3)
- Business Associations Fall 2010 Fendler OutlineDocument121 pagesBusiness Associations Fall 2010 Fendler OutlineJoshua Ryan Collums100% (1)
- CAP Regulation 20-1 - 05/29/2000Document47 pagesCAP Regulation 20-1 - 05/29/2000CAP History LibraryNo ratings yet
- Bancassurance Black Book Rahul 777-2Document62 pagesBancassurance Black Book Rahul 777-2Shubham ShahNo ratings yet
- Mapping Groundwater Recharge Potential Using GIS-Based Evidential Belief Function ModelDocument31 pagesMapping Groundwater Recharge Potential Using GIS-Based Evidential Belief Function Modeljorge “the jordovo” davidNo ratings yet
- Cars Should Be BannedDocument3 pagesCars Should Be BannedIrwanNo ratings yet
- Corruption in PakistanDocument15 pagesCorruption in PakistanklutzymeNo ratings yet
- CCT AsqDocument12 pagesCCT Asqlcando100% (1)
- Meanwhile Elsewhere - Lizzie Le Blond.1pdfDocument1 pageMeanwhile Elsewhere - Lizzie Le Blond.1pdftheyomangamingNo ratings yet
- Indian Institute of Management KozhikodeDocument5 pagesIndian Institute of Management KozhikodepranaliNo ratings yet
- Diana's Innermost House: MagazineDocument42 pagesDiana's Innermost House: MagazinealexgoagaNo ratings yet
- Case Study - Soren ChemicalDocument3 pagesCase Study - Soren ChemicalSallySakhvadzeNo ratings yet
- Denial and AR Basic Manual v2Document31 pagesDenial and AR Basic Manual v2Calvin PatrickNo ratings yet
- ZOOLOGY INTRODUCTIONDocument37 pagesZOOLOGY INTRODUCTIONIneshNo ratings yet
- BS EN 364-1993 (Testing Methods For Protective Equipment AgaiDocument21 pagesBS EN 364-1993 (Testing Methods For Protective Equipment AgaiSakib AyubNo ratings yet
- Green Management: Nestlé's Approach To Green Management 1. Research and DevelopmentDocument6 pagesGreen Management: Nestlé's Approach To Green Management 1. Research and DevelopmentAbaidullah TanveerNo ratings yet
- Continuation in Auditing OverviewDocument21 pagesContinuation in Auditing OverviewJayNo ratings yet
- CASE DigeSTDocument2 pagesCASE DigeSTZepht BadillaNo ratings yet
- Logistic Regression to Predict Airline Customer Satisfaction (LRCSDocument20 pagesLogistic Regression to Predict Airline Customer Satisfaction (LRCSJenishNo ratings yet
- Conplast SP430 0407Document4 pagesConplast SP430 0407Harz IndNo ratings yet
- 3 Course Contents IIIBDocument5 pages3 Course Contents IIIBshahabNo ratings yet
- 4.5.1 Forestry LawsDocument31 pages4.5.1 Forestry LawsMark OrtolaNo ratings yet
- Introduction To Elective DesignDocument30 pagesIntroduction To Elective Designabdullah 3mar abou reashaNo ratings yet
- Binaural Recording Technology: A Historical Review and Possible Future DevelopmentsDocument22 pagesBinaural Recording Technology: A Historical Review and Possible Future DevelopmentsNery BorgesNo ratings yet
- Las Q1Document9 pagesLas Q1Gaux SkjsjaNo ratings yet
- Defect Prevention On SRS Through ChecklistDocument2 pagesDefect Prevention On SRS Through Checklistnew account new accountNo ratings yet
- Resume Ajeet KumarDocument2 pagesResume Ajeet KumarEr Suraj KumarNo ratings yet
- Module 5Document10 pagesModule 5kero keropiNo ratings yet