Professional Documents
Culture Documents
Lecture Notes For: Solid State Electronic Devices: With Modifications by M. Nadeem Akram and Per Ohlckers
Uploaded by
Saleha QuadsiaOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Lecture Notes For: Solid State Electronic Devices: With Modifications by M. Nadeem Akram and Per Ohlckers
Uploaded by
Saleha QuadsiaCopyright:
Available Formats
Lecture notes for:
Solid State Electronic Devices
by S. Banerjee
with modifications by M. Nadeem Akram and Per Ohlckers
The most important topics in the
syllabus:
Crystal structure of semiconductors
Quantum physics
Bandstructure, carrier drift
Optical Generation-Recombination,
Diffusion
Bipolar (PN) junctions
Field Effect Transistors: MOS ICs
Bipolar Junction Transistors
Optoelectronics
Chapter 1 and 2 slides in this file
Moores Law:
Exponential increase of
transistor count, and
decrease of sizes with time
Chapter 1
2
Slide 3
Semiconductors
Periodic Table
l = 1 (p)
l = 0 (s)
l = 2 (d)
l = 3 (f)
1
2
3
4
5
6
7
N
o
b
l
e
G
a
s
H
a
l
o
g
e
n
G
r
o
u
p
V
I
G
r
o
u
p
I
V
G
r
o
u
p
V
G
r
o
u
p
I
I
I
n
4
5
6
In addtion; Ternary and quartenary
semiconductors are used in specific applications
Examples of ternary semiconductors: AlxGa1-xAs, GaAsyP1-y
Example of quartenary semiconductors: AlxGa1-xAsyP1-y
Silicon (Si) (Elementary semiconductor) is by far the most
used material for integrated circuits combining excellent
technical perforance with low cost.
Gallium Arsenide (GaAs) (Binary semiconductor) is important
in optoelectronics, favourably combining electronic and
optical features.
A LATTICE is an infinite, periodic arrangement of points. The symmetry
determines the lattice, not the magnitudes of the distances.
At each lattice point if we put a physical entity or BASIS which is one atom (or
a group of atoms in the same arrangement), we get a CRYSTAL.
A crystal has long range order, polycrystalline material only short range order
and an amorphous material no order.
7
Crystal Lattice
PRIMITIVE cell ODEF is the smallest cell that can be translated by integer
number of primitive vectors a and b to replicate the lattice. It has lattice
points ONLY at corners of cell. It is not unique but convention is to choose
smallest and most orthogonal primitive vectors.
UNIT cell (rectangle) allows lattice points at corners, face center and body
center in 3-D. It is sometimes used instead of the primitive cell if it can
represent the symmetry of the lattice better. (in this example centered
rectangular 2-D lattice). It replicates the lattice by integer translations of
basis vectors.
8
Primitive Cell/Unit Cell
3-D lattices are called SPACE lattices or Bravais lattices.
These are examples of cubic UNIT cells because they obey
POINT symmetry operations (reflection, rotation, inversion) of a
cube.
The PRIMITIVE cells are different: It is cubic for the SC case,
but non-cubic for FCC and BCC. The primitive cell has only ONE
lattice point per cell, and a volume of 1/n if n is the number
density of points.
9
Space lattices or Bravais lattices
1. Choose coordinate system with origin at any lattice point and orient axes
along edges of cube.
2. Determine intercepts of planes with axes in multiples of unit cell edges.
3. Take reciprocals of intercepts and reduce to lowest set of integers, unless
intercept is fraction of unit cell edge
4. Equivalent sets of (100) planes: ({100} planes) by rotation of the unit cell
within the cubic lattice.
Miller Indices for Planes
10
1. Fix coordinate system and choose vector along direction in the lattice.
2. Determine components of vector along axes.
3. Reduce to lowest set of integers.
4. Equivalent [100] directions indicated as <100>.
Miller Indices for Directions
11
If all the atoms are the same as in Si or Ge, it is a diamond structure. If the
nearest neighbor atoms are different as in GaAs,it is zinc blende. The 4
nearest neighbors are shown in a symmetric, tetrahedral arrangement.
Diamond lattice
structure:
(a) a unit cell of the
diamond lattice
constructed by placing
atoms from each atom in
an fcc; (b) top view
(along any 100 direction)
of an extended diamond
lattice. The colored
circles indicate one fcc
sublattice and the black
circles indicate the
interpenetrating fcc.
12
13
Packing fraction:
Si Unit Cell shown
14
Number density:
Si Unit Cell shown
15
--->
The 3 most important
Silicon Crystal Planes
Pull crystal SLOWLY (~ mm/minute) while rotating (for uniformity). Diameter
increases as pull rate reduced. Industry grows large 300 mm diameter boules
or ingots. Few stress-related defects because crystal unconstrained.
Molten Si at 1412 C. Add dopants to melt, but incorporation governed by
distribution coefficient or segregation coefficient, k
d
= C
S
/C
L
. Common
impurities are C and O from crucible.
Czochralski Bulk Crystal Growth
Steps in (100) Si wafer fabrication:
1. Grind boule into cylinder and put
notch on {110}orientation.
2. Saw into wafers, and grinding/
polishing of damage.
3. Chamfer edges and chemical-
mechanical polish front.
Ref: Plummer
16
Atmospheric pressure CVD systems. The Si wafers are held in slots cut on the
sides of a SiC-coated graphite susceptor that flares out near the base to
promote gas flow patterns conducive to uniform epitaxy. Typical precursors and
deposition temperatures are SiCl
4
(1200 C) and SiH
2
Cl
2
(1000 C).
Metal Organic CVD (MOCVD) for III-V semiconductors.
Barrel-type reactor for Si Vapor Phase Epitaxy
17
Crystal growth by
molecular beam epitaxy
(MBE):
(a) evaporation cells inside a
high -vacuum chamber
(10
-11
Torr) directing
beams of Al, Ga, As, and
dopants onto a GaAs
substrate at ~600C;
(b) (b) scanning electron
micrograph of the cross
section of superlattice of
GaAs (dark lines) and
AlGaAs (light lines).
Each layer is four
monolayers thick.
18
1-D: Heteroepitaxy and misfit
dislocations due to lattice mismatch
between SiGe and Si leading to
compressive strain in the SiGe layer.
(a) For less than critical layer
thickness, t
c
, pseudomorphic growth
occurs; (b) above t
c
, misfit
dislocations form at the interface.
Crystal Defects
Ref: Plummer
0-D: Vacancy (missing atom);
Interstitial (extra atom in void);
Impurity- substitutional/interstitial
1-D Dislocation
2-D: Surface, stacking fault
3-D: Precipitate or cluster
19
Chapter 2: Quantum Physics
Diffraction can only be explained by
treating light as a wave instead of a
particle, supporting Huygens over Newton.
()(v) = c = 3 x 10
8
m/s
= speed of light (constant)
Characterized by: Wavelength or Frequency;
Amplitude (A) or Intensity (=A
2
), and Phase
Planck/Einstein- Light Quanta Photons
Planck found that in order to
model black body radiation,
one has to envision that
energy (in the form of light)
is lost (or gained) in integer
values according to:
AE = nhv
Energy Change
n = 1, 2, 3 (integers)
frequency
h = Plancks constant = 6.626 x 10
-34
J.s
E
photon
= hv
21 Slide
Photoelectric Effect- Einstein
2
1
2
e photon
m h q v v = u
Energy needed to release electron =
workfunction of metal (measured in eV or J)
Light apparently behaves both as a particle and a wave: wave-particle duality.
Perhaps so does matter?? Leads to quantum mechanics
0
v
0
Frequency ( v)
metal
One needs a minimum amount of photon
energy to see electrons.
Also for v v
o
, number of electrons increases
linearly with light intensity.
As frequency of incident light is increased,
kinetic energy of emitted e
-
increases linearly.
Continuous spectrum from solids
Quantized spectrum from atoms
A
E
A
E
23
Only certain AE are allowed
Any AE is possible
Slide
Rydbergs Model
Rydberg extends the Balmer model (n
1
=2) for visible spectra to other
spectral series.
|
|
.
|
\
|
=
2
2
2
1
1 1
n n
R
y
v
n
1
= 1, 2, 3, ..
n
2
= n
1
+1, n
1
+2,
R
y
= 3.29 x 10
15
1/s
This suggests that the energy levels of the H atom are
proportional to 1/n
2
Ritz discovers the combinatorial principle between
photon frequencies.
Hydrogen Atom Models
Rutherford proposed a planetary model
where the light, negative electrons orbit
around a heavy nucleus made up of
positive protons and neutral neutrons.
He placed no restrictions on electron
orbits, which was a problem because
according to Maxwell such orbiting
electrons should lose energy and
combine with nucleus.
1. Bohr proposed that electrons can
only have certain allowed orbits.
2. In these orbits, the angular
momentum is quantized as:
p = mvr = nh/2
3. Electrons can lose or gain energy
only during transitions between these
orbits.
AE = E
i
-E
f
= hv
25
26
Hydrogen Atom
Models
De Broglie Waves
Based on wave-particle duality of matter, de Broglie suggested that particles have a
wavelength given by:
mv
h
p
h
= =
not allowed
k
h h
p = = =
t
t
2
2 mv
h
p
h
= =
The Bohr orbits satisfied the standing wave condition
t n
mv
h
n r = = 2
p = mvr = nh/2
27 Slide
Heisenberg Uncertainty Principle
Another limitation of classical physics was that it assumed we could know both
the position and momentum of an electron exactly.
Heisenberg development of quantum mechanics led him to the observation that
there is a fundamental limit to how well one can know both the position and
momentum of a particle simultaneously.
t 4
h
t E > A - A
t 4
h
p x x > A - A
Uncertainty in position
Uncertainty in momentum
Similar uncertainties in y,z.
4
th
uncertainty relation
What is the uncertainty in momentum for an electron in a 1 radius
orbital in which the positional uncertainty is 1% of the radius.?
Ap =
h
4tAx
=
6.626x10
34
J.s
( )
4t 1x10
12
m
( )
= 5.27x10
23
kg.m/ s
28 Slide
Quantum Mechanics: Schrodinger equation
Schrodinger developed a mathematical formalism
that incorporated the wave nature of matter:
( - greek letter Psi pronounced (p)sigh)
( H - greek letter Eta pronounced ay-tay)
H = E
H
The Hamiltonian:
=
p
2
2m
+ (PE)
Kinetic Energy
operating on
the Wavefunction:
gives us the
total energy
x
E = energy
What is an
operator?
e.g. derivatives
d/dt or d
2
/dx
2
Schrodinger equation:
Wavefunction
What is a wavefunction?
= a probability amplitude (complex)
Consider a wave:
( ) ( ) tv +
=
t kx j
Ae y
2
( ) ( )
( )
( ) ( )
( )
2 2 2 *
2
A Ae e A y
t kx j t kx j
= =
+ + tv tv
Intensity =
Probability of finding a particle in space:
Probability =
With the normalized wavefunction, we can
describe spatial distributions.
31
( )
) (
kx j
Ae x
+
=
( )
t j
E t x V
x m
H
c
c
= =
(
+
c
c
=
,
2
2
2 2
Time evolution of wavefunction in 1-D given by Schrodinger equation, where
Hamiltonian is H = KE+ PE=T +V
t j
Et
j
e e t f
t Ef
t
t f
j
e
= =
=
c
c
) (
) (
) (
Use separation of variables, for static potential V(x):
) ( ) (
) ( ) (
) ( ) ( ) V(
2
2
2 2
t f x E
t
t f x
j
t f x x
x m
=
c
c
=
(
+
c
c
Get time-independent Schrodinger
eigenvalue equation for spatial part:
For free particle, V=0 putting:
m
k
E
2
2 2
=
32
k =
h
=
( )
) (
,
t kx j
Ae t x
e
+
=
e
c
c
= = =
=
m
p
m
k
t j
E
2 2
2 2 2
For a free particle, multiplying the spatial and temporal parts of the
solution we get a plane wave function of position, x, and time, t,
with normalization constant A, wavevector k and frequency :
(Planck)
(de Broglie)
= p
Expectation values of quantum mechanical
operators correspond to physical quantities.
c
c
x j
33
Particle in a potential well and Quantization
( ) |
.
|
\
|
=
L
x n
L
x
t
sin
2
( )
|
.
|
\
|
=
L
x n
L
x
t
sin
2
( ) ( ) kx A x sin =
Energy is quantized
in terms of quantum
number n due to
confinement of particle.
-
E
2
2 2
8mL
h n
E =
n = 1, 2,
x
0
inf.
0 L
34 Slide
(a) Potential barrier of height V
0
and thickness
W;
(b) (b) probability density for an electron with
energy E < V
0
, indicating a non-zero value of
the wave function beyond the barrier.
Quantum mechanical tunneling
35
Quantization in Spherically Symmetric Potentials
In the case of the hydrogen atom, energy
becomes quantized due to the presence of a
constraining potential.
r
0
Schrodinger
Equation
r
Ze
r V
2
) (
=
0
Recovers the Bohr model
36 Slide
H-atom wavefunctions
If we solve the Schrodinger equation using this
potential, we find that the energy levels are
quantized:
E
n
=
Z
2
n
2
me
4
8c
0
2
h
2
|
\
|
.
|
= 2.178x10
18
J
Z
2
n
2
|
\
|
.
|
n is the principal quantum number, and ranges
from 1 to infinity.
These correspond to the Bohr orbits,
and is due to constraining Coulomb potential.
2
18 18
2
2.178 10 2.178 10 13.6 1( )
n
Z
E x J x J eV for n Rydberg
n
| |
= = = =
|
\ .
H-atom wavefunctions- orbitals
In solving the Schrodinger equation, other quantum numbers become evident:
l, the orbital angular momentum quantum number. Gives ellipticity of orbit.
m, the z component of orbital angular momentum.
Ranges in value from -l to 0 to l. Lines up along external magnetic field.
We can then characterize the wavefunctions based on
the quantum numbers (n, l, m, s).
Also have a spin quantum number s of
l (0 to (n-1)) is given a letter value as follows:
0 = s (sharp)
1 = p (principal)
2 = d (diffuse)
3 = f (fundamental)
n l Orbital m
l
# of Orb.
1 0 1s 0 1
2 0 2s 0 1
1 2p -1, 0, 1 3
3 0 3s 0 1
1 3p -1, 0, 1 3
2 3d -2, -1, 0, 1, 2 5
For each of these, have spin s = .
The total number of electrons in the shells are 2, 8, 18,..
Orbital energies increase as 1/n
2
Orbitals of same n, but different
l are considered to be of (almost)
equal energy (degenerate).
39 Slide
S (l=0) Orbital Shapes
r dependence only
as n increases, orbitals
demonstrate n-1 nodes.
1s
=
1
t
Z
a
o
|
\
|
.
|
3
2
e
Z
a
0
r
=
1
t
Z
a
o
|
\
|
.
|
3
2
e
o
a
0
is the Bohr radius = 0.53
2p (l = 1) orbital shapes
not spherical, but lobed.
labeled with respect to orientation along x, y, and z.
2p
z
=
1
4 2t
Z
a
o
|
\
|
.
|
3
2
oe
o
2
cosu
Electronic Structure of Elements and Periodic Table
1A 2A 3A 4A 5A 6A 7A 8A
1
H
1s
1
2
He
1s
2
3
Li
1s
2
2s
1
4
Be
1s
2
2s
2
5
B
1s
2
2s
2
2p
1
6
C
1s
2
2s
2
2p
2
7
N
1s
2
2s
2
2p
3
8
O
1s
2
2s
2
2p
4
9
F
1s
2
2s
2
2p
5
10
Ne
1s
2
2s
2
2p
6
11
Na
[Ne]
3s
1
12
Mg
[Ne]
3s
2
13
Al
[Ne]
3s
2
3p
1
14
Si
[Ne]
3s
2
3p
2
15
P
[Ne]
3s
2
3p
3
16
S
[Ne]
3s
2
3p
4
17
Cl
[Ne]
3s
2
3p
5
18
Ar
[Ne]
3s
2
3p
6
Lowest energy orbitals occupied first: also Pauli exclusion principle
42 Slide
Electronic structure and energy levels in a Si atom: (a) The orbital model of a Si atom
showing the 10 core electrons (n = 1 and 2), and the 4 valence electrons (n = 3); (b)
energy levels in the coulombic potential of the nucleus are also shown schematically.
Atomic number, Z= 14= number of protons or electrons; atomic weight, A= number of
protons plus neutrons.e.g. one isotope of Si is
14
Si
28
43
The spherically symmetric s type wave functions or orbitals are
positive everywhere, while the three mutually perpendicular p
type orbitals ( p
x
, p
y
, p
z
) are dumbbell shaped and have a
positive lobe and a negative lobe. The four sp
3
hybridized
orbitals, only one of which is shown here, point symmetrically in
space and lead to the diamond lattice in Si.
Hybridized Orbitals in a Si Atom
44
End of Chapter 1 and 2 slides
Most important topics:
To be included later
You might also like
- Bohr Model of The Hydrogen AtomDocument27 pagesBohr Model of The Hydrogen AtomgalaxybazaarNo ratings yet
- The Philosophy of Quantum PhysicsDocument304 pagesThe Philosophy of Quantum Physicsסמואל פיליפ100% (1)
- Microelectronics TechDocument33 pagesMicroelectronics TechmailstonaikNo ratings yet
- Quantum PhysicsDocument122 pagesQuantum PhysicsYang Xu100% (2)
- Introduction To Quantum Field TheoryDocument261 pagesIntroduction To Quantum Field TheorykoutariNo ratings yet
- 3.2.1 Example - WBS, V 1.0.1Document3 pages3.2.1 Example - WBS, V 1.0.1Saleha Quadsia100% (1)
- Atomic Structure - Network Solids Part 1 2Document60 pagesAtomic Structure - Network Solids Part 1 2eiwk100% (1)
- Carlo Rovelli - Loop Quantum Gravity PDFDocument69 pagesCarlo Rovelli - Loop Quantum Gravity PDFioan dumitrescuNo ratings yet
- Diet Plan Week 1: Breakfast Lunch Dinner Snacks ExerciseDocument16 pagesDiet Plan Week 1: Breakfast Lunch Dinner Snacks ExerciseSaleha QuadsiaNo ratings yet
- MCQs Nuclear Analytical Techniques MSC 4THDocument11 pagesMCQs Nuclear Analytical Techniques MSC 4THPhoton Online Science Academy100% (1)
- 5-X Ray DiffractionDocument24 pages5-X Ray DiffractionYagnesh Rohit100% (1)
- Activity 2.2 Atomic Orbitals - S2-2015Document10 pagesActivity 2.2 Atomic Orbitals - S2-2015Devandra Eko RadityoNo ratings yet
- Structure of Atom Sub-Atomic ParticlesDocument9 pagesStructure of Atom Sub-Atomic ParticlesSunil PandeyNo ratings yet
- XI-Chemistry-DOE Support Material 2019-20 - 2Document22 pagesXI-Chemistry-DOE Support Material 2019-20 - 2MeersNo ratings yet
- EE145 HMWK 3 SolDocument8 pagesEE145 HMWK 3 SolNuwan SameeraNo ratings yet
- Practice Midterm 2Document10 pagesPractice Midterm 2jesi5445No ratings yet
- Atomic Structure: Kotz CH 7 & CH 22 (Sect 4,5)Document37 pagesAtomic Structure: Kotz CH 7 & CH 22 (Sect 4,5)Anonymous JamqEgqqh1No ratings yet
- From Atoms To Solids: Jeffrey C. GrossmanDocument44 pagesFrom Atoms To Solids: Jeffrey C. Grossmanchethugowda7No ratings yet
- Eng323 Lect01 MyDocument45 pagesEng323 Lect01 MyAndrea MorenoNo ratings yet
- Chapter 12 - Atoms-Saju-Hsslive PDFDocument9 pagesChapter 12 - Atoms-Saju-Hsslive PDFAmiNo ratings yet
- Atomic Structure: Wave/Particle ConceptDocument51 pagesAtomic Structure: Wave/Particle ConceptLita W NirmalasariNo ratings yet
- Chapter 28 Atomic Physics: The Hydrogen Atom The Bohr Model Electron Waves in The AtomDocument64 pagesChapter 28 Atomic Physics: The Hydrogen Atom The Bohr Model Electron Waves in The Atomvivekrajbhilai5850No ratings yet
- Material Science Unit-1: Me - Iii SemDocument48 pagesMaterial Science Unit-1: Me - Iii SemSangitabangaNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: Ja (j-1) A (j+1) ADocument9 pages2.57 Nano-to-Macro Transport Processes Fall 2004: Ja (j-1) A (j+1) AcaptainhassNo ratings yet
- The Crystalline Solid StateDocument58 pagesThe Crystalline Solid Stated-fbuser-65596417No ratings yet
- Mosfet Chapter - 1Document48 pagesMosfet Chapter - 1田佳生No ratings yet
- ME F213 & MF F213 Materials Science & EngineeringDocument43 pagesME F213 & MF F213 Materials Science & EngineeringTarun KumarNo ratings yet
- 2479 Chap01Document44 pages2479 Chap01Xavier Kattukulam0% (1)
- Sri Chaitanya Iit Academy: Work SheetDocument8 pagesSri Chaitanya Iit Academy: Work SheetLisa ParkerNo ratings yet
- The Crystalline Solid StateDocument58 pagesThe Crystalline Solid Statearamki1No ratings yet
- Notes On Semiconductor Physics For Electronic DevicesDocument27 pagesNotes On Semiconductor Physics For Electronic DevicesspyseetunaNo ratings yet
- Semiconductor Devices . Lecture 1 ... Prof - Dr.Abdulhadi AL-OgailiDocument8 pagesSemiconductor Devices . Lecture 1 ... Prof - Dr.Abdulhadi AL-OgailiWesam WesamNo ratings yet
- Atomic Structure and PeriodicityDocument75 pagesAtomic Structure and PeriodicityTheodorNo ratings yet
- Atomic Structure 10feb07Document27 pagesAtomic Structure 10feb07Fredrick MutungaNo ratings yet
- Basic Semiconductor PhysicsDocument311 pagesBasic Semiconductor PhysicseeshgargNo ratings yet
- Structure of Atom - Class 11thDocument38 pagesStructure of Atom - Class 11thAdil KhanNo ratings yet
- Chapter 8 Atomic StructureDocument68 pagesChapter 8 Atomic StructureHaqnawaz100% (1)
- Bonding Crystal Structure 2012 FallDocument6 pagesBonding Crystal Structure 2012 FallHanksalsaNo ratings yet
- Homework Set3 ParticlenatureofmatterDocument2 pagesHomework Set3 Particlenatureofmatteryobrosky0% (1)
- Pauli TrapDocument6 pagesPauli TrapMichael MurphyNo ratings yet
- Inorganic Chem. I Ch. 1Document98 pagesInorganic Chem. I Ch. 1Shifa GhannamNo ratings yet
- G. W. Watson - An Introduction To Molecular Orbital TheoryDocument28 pagesG. W. Watson - An Introduction To Molecular Orbital TheoryNuansak3No ratings yet
- Previous Hse Questions and Answers of The Chapter "Structure of Atom"Document12 pagesPrevious Hse Questions and Answers of The Chapter "Structure of Atom"YADUKRISHNAN K NAIRNo ratings yet
- Electronic Structure of AtomsDocument29 pagesElectronic Structure of AtomsTiara MejicaNo ratings yet
- Edx Ebsd MSC EnglDocument51 pagesEdx Ebsd MSC EnglSócrates NajarNo ratings yet
- Assignment EDocument2 pagesAssignment EWilson Jones0% (1)
- Basics of Lanthanide PhotophysicsDocument45 pagesBasics of Lanthanide PhotophysicsAngela StefanNo ratings yet
- Hsslive-Xi-Chem-Prvs-Qn-2. Structure of Atom Q & ADocument13 pagesHsslive-Xi-Chem-Prvs-Qn-2. Structure of Atom Q & Aaromalssatheesh02No ratings yet
- Structure of Atom: Sub-Atomic Particles: Name Symbol Charge/C Relative Charge Mass/kgDocument8 pagesStructure of Atom: Sub-Atomic Particles: Name Symbol Charge/C Relative Charge Mass/kgSparsh MehtaNo ratings yet
- X-Ray DiffractionDocument30 pagesX-Ray DiffractionMerve Ayvaz KöroğluNo ratings yet
- Solution To Question Paper IV, V.U. 2013Document9 pagesSolution To Question Paper IV, V.U. 2013Abhijit Kar GuptaNo ratings yet
- Crystallography and Structure - Ch3F10-2Document66 pagesCrystallography and Structure - Ch3F10-2Syeda Fatima FarzamNo ratings yet
- 3.EC Handout NotesDocument48 pages3.EC Handout NotesHimanshuuuuNo ratings yet
- CBSE Sample Paper Class 12 Physics Set 3: All Questions Are Compulsory. There Are 27 Questions in AllDocument4 pagesCBSE Sample Paper Class 12 Physics Set 3: All Questions Are Compulsory. There Are 27 Questions in AllI dont have a NameNo ratings yet
- STPM Chemistry Form 6Document5 pagesSTPM Chemistry Form 6BabasChong100% (1)
- Lecture 5 & 6 - Electronic Structure of AtomsDocument43 pagesLecture 5 & 6 - Electronic Structure of Atomsapi-19824406No ratings yet
- OrbitalsDocument40 pagesOrbitalsEmilyNo ratings yet
- Atoms (4 Lecture)Document172 pagesAtoms (4 Lecture)kumarchandanyadav276No ratings yet
- Basic Atomic Theory and Atomic Orbitals: 2 Meet On Chemical Bond CourseDocument32 pagesBasic Atomic Theory and Atomic Orbitals: 2 Meet On Chemical Bond CourseAditya AdityaNo ratings yet
- ACFrOgC xiuXYskoUCylB1F9L1IEJcj Ta KoLk6CTvaGqltDFWA2qAIKTeqUvP 0 7U6kDWb0J0D4WA8tzfPGbl3oDF5E2WbfWJwsRiEHl3syXtQRSt2h85SwNwBgDocument71 pagesACFrOgC xiuXYskoUCylB1F9L1IEJcj Ta KoLk6CTvaGqltDFWA2qAIKTeqUvP 0 7U6kDWb0J0D4WA8tzfPGbl3oDF5E2WbfWJwsRiEHl3syXtQRSt2h85SwNwBgJihanaisyNo ratings yet
- 1-4 X-Ray Characterization of MaterialsDocument27 pages1-4 X-Ray Characterization of MaterialsDr. Saad B. H. Farid0% (1)
- Electronic Conf. Atomic, Ionicsize PDFDocument10 pagesElectronic Conf. Atomic, Ionicsize PDFAtul GautamNo ratings yet
- Elec DiffDocument8 pagesElec DiffMillaChemNo ratings yet
- PH 310 SlidesDocument44 pagesPH 310 SlidesBushra IbrahimNo ratings yet
- Ex ExpPhys V WS2006 07ENDocument15 pagesEx ExpPhys V WS2006 07ENSatyam AgrahariNo ratings yet
- Biomass and Bioenergy: Research PaperDocument18 pagesBiomass and Bioenergy: Research PaperSaleha QuadsiaNo ratings yet
- Effects of Sulphur and Zinc Applications On Growth and Nutrition of Bread Wheat in Calcareous Clay Loam SoilDocument7 pagesEffects of Sulphur and Zinc Applications On Growth and Nutrition of Bread Wheat in Calcareous Clay Loam SoilSaleha QuadsiaNo ratings yet
- Journal of The Energy Institute: Adisak Pattiya, Suntorn SuttibakDocument10 pagesJournal of The Energy Institute: Adisak Pattiya, Suntorn SuttibakSaleha QuadsiaNo ratings yet
- Supplementary Material: For ManuscriptDocument15 pagesSupplementary Material: For ManuscriptSaleha QuadsiaNo ratings yet
- The Impact of Accounting Information Systems AIS oDocument20 pagesThe Impact of Accounting Information Systems AIS oSaleha QuadsiaNo ratings yet
- Basic Challenges of Organizational DesignDocument48 pagesBasic Challenges of Organizational DesignSaleha QuadsiaNo ratings yet
- Course Schedule2014 PreliminaryDocument1 pageCourse Schedule2014 PreliminarySaleha QuadsiaNo ratings yet
- Eigenfrequencies and Q Factor in The Geometrical Theory of Whispering-Gallery ModesDocument6 pagesEigenfrequencies and Q Factor in The Geometrical Theory of Whispering-Gallery ModesSaleha QuadsiaNo ratings yet
- Au-Sn SLID Bonding EMPC2009 PresentationDocument17 pagesAu-Sn SLID Bonding EMPC2009 PresentationSaleha Quadsia100% (1)
- Conflict Studies Research CentreDocument10 pagesConflict Studies Research CentreSaleha QuadsiaNo ratings yet
- Hall Effect Measurements Essential For Characterizing High Carrier MobilityDocument4 pagesHall Effect Measurements Essential For Characterizing High Carrier MobilitySaleha QuadsiaNo ratings yet
- Spin LiquidDocument60 pagesSpin LiquidDyvison PimentelNo ratings yet
- Models of Light Student WorksheetDocument3 pagesModels of Light Student WorksheetRico T. MusongNo ratings yet
- Quantum Cold-Case Mysteries Revisited 2Document39 pagesQuantum Cold-Case Mysteries Revisited 2John SmithNo ratings yet
- Chem Final ExamDocument42 pagesChem Final ExamWild RiftNo ratings yet
- Band Theory of MetalsDocument3 pagesBand Theory of MetalsShirley DasNo ratings yet
- Gennaro Auletta Quantum Mechanics and ContingencyDocument7 pagesGennaro Auletta Quantum Mechanics and ContingencyÁlvaro Riobóo de LarrivaNo ratings yet
- Ivantchenko - GEANT4 LOW ENERGY Geant4 EM PackagesDocument34 pagesIvantchenko - GEANT4 LOW ENERGY Geant4 EM PackagesForeverSleepingNo ratings yet
- 14d-Modern FR Practice Problems-ANSWERSDocument17 pages14d-Modern FR Practice Problems-ANSWERSStan MazoNo ratings yet
- Dimensional Regularization: NotesDocument2 pagesDimensional Regularization: NotesAtikshaNo ratings yet
- Liquid Drop ModelDocument26 pagesLiquid Drop ModelBibhu Prasad SahooNo ratings yet
- Time Symmetry and The Einstein Paradox.: Institut Henri Poincar - Rue Pierre Et Marie Curie, ParisDocument24 pagesTime Symmetry and The Einstein Paradox.: Institut Henri Poincar - Rue Pierre Et Marie Curie, PariscdcrossroaderNo ratings yet
- The Dirac Equation For The ElectronDocument29 pagesThe Dirac Equation For The ElectronJK1434No ratings yet
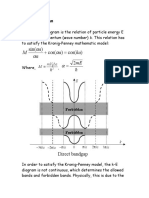
- ka a a a M:) cos cos sin (= + αDocument5 pageska a a a M:) cos cos sin (= + αFaizan ArshadNo ratings yet
- Millikan ExperimentDocument16 pagesMillikan ExperimentBhaskar TupteNo ratings yet
- The Trouble With PhysicsDocument16 pagesThe Trouble With PhysicsGerson MonteiroNo ratings yet
- Chem12 c03 3 3Document5 pagesChem12 c03 3 3Eric McMullenNo ratings yet
- The Nuclear Atom 3 MSDocument4 pagesThe Nuclear Atom 3 MSmuhammadzariyanshafiqueNo ratings yet
- Premios NobelDocument3 pagesPremios NobelDanna Valentina Medina SanchezNo ratings yet
- Mariel Vazquez - Analyzing DNA Topology With Mathematical and Computational MethodsDocument20 pagesMariel Vazquez - Analyzing DNA Topology With Mathematical and Computational MethodsLokosooNo ratings yet
- Question Bank Atomic Structure: An Atom Uncharged ?Document13 pagesQuestion Bank Atomic Structure: An Atom Uncharged ?Tanay GuptaNo ratings yet
- Introduction PDFDocument9 pagesIntroduction PDFMahendra SankhuaNo ratings yet
- Nuclei in One Shot - Class Notes - LEC-6 - PPT-6 - Physics - Nuclei - Vijeta Series - Kshitiz Kanik Sir - RAM NIWASDocument61 pagesNuclei in One Shot - Class Notes - LEC-6 - PPT-6 - Physics - Nuclei - Vijeta Series - Kshitiz Kanik Sir - RAM NIWASprajwal jhaNo ratings yet
- Quantum NumbersDocument2 pagesQuantum NumbersWong Weng SiongNo ratings yet
- LAS No. 4 Formation of Elements Heavier Than IronDocument2 pagesLAS No. 4 Formation of Elements Heavier Than IronWarren OlemberioNo ratings yet
- Physics 127a: Class Notes: Lecture 17: Ideal Fermi GasDocument7 pagesPhysics 127a: Class Notes: Lecture 17: Ideal Fermi GasShweta SridharNo ratings yet
- Electricity NotesDocument4 pagesElectricity NotesmeowNo ratings yet