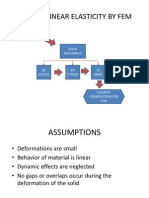
MANE 4240 & CIVL 4240

Introduction to Finite Elements

Introduction to 3D
Elasticity
Prof. Suvranu De
Reading assignment:
Appendix C+ 6.1+ 9.1 + Lecture notes
Summary:
3D elasticity problem
Governing differential equation + boundary conditions
Strain-displacement relationship
Stress-strain relationship
Special cases
2D (plane stress, plane strain)
Axisymmetric body with axisymmetric loading
Principle of minimum potential energy
1D Elasticity (axially loaded bar)
x
y
x=0
x=L
A(x) = cross section at x
b(x) = body force distribution
(force per unit length)
E(x) = Youngs modulus
u(x) = displacement of the bar
at x
x
1. Strong formulation: Equilibrium equation + boundary
conditions
L x b
dx
d
! 0 ; 0
o
L x at F
dx
du
EA
x at u
! !
! ! 0 0
Boundary conditions
Equilibrium equation
F
3. Stress-strain (constitutive) relation :
(x) E (x) =
E: Elastic (Youngs) modulus of bar
2. Strain-displacement relationship:
dx
du
(x) =
Problem definition
3D Elasticity
x
y
z
Surface (S)
Volume (V)
u
v
w
x
V: Volume of body
S: Total surface of the body
The deformation at point
x =[x,y,z]
T
is given by the 3
components of its
displacement

|
!
w
v
u
u
NOTE: u= u(x,y,z), i.e., each
displacement component is a function
of position
3D Elasticity:
EXTERNAL FORCES ACTING ON THE BODY
Two basic types of external forces act on a body
1. Body force (force per unit volume) e.g., weight, inertia, etc
2. Surface traction (force per unit surface area) e.g., friction
BODY FORCE
x
y
z
Surface (S)
Volume (V)
u
v
w
x
X
a
dV
X
b
dV
X
c
dV
Volume
element dV Body force: distributed
force per unit volume (e.g.,
weight, inertia, etc)

!
c
b
a
X
X
X
X
NOTE: If the body is accelerating,
then the inertia force
may be considered as part of X

!
w



V
V
V
V v
u
u
u
~
V ! X X
x
y
z
S
T
Volume (V)
u
v
w
x
X
a
dV
X dV
X
c
dV
Volume
element dV
p
y
p
z
p
x
Traction: Distri uted
force per unit surface
area

!
z
y
x
p
p
p
T
S
SURFACE TRACTION
3D Elasticity:
INTERNAL FORCES
If I take out a chunk of material from the body, I will see that,
due to the external forces applied to it, there are reaction
forces (e.g., due to the loads applied to a truss structure, internal
forces develop in each truss member). For the cube in the figure,
the internal reaction forces per unit area(red arrows) , on each
surface, may be decomposed into three orthogonal components.
x
y
z
Volume (V)
u
v
w
x
Volume
element dV
W
x
W
y
W
z
X
yz
X
yx
X
xy
X
xz
X
zy
X
zx
3D Elasticity

|
=
zx
yz
xy
z
y
x
X
X
X
W
W
W
W
x
y
z
W
x
W
y
W
z
X
yz
X
yx
X
xy
X
xz
X
zy
X
zx
W
x
, W
y
and W
z
are normal stresses.
The rest 6 are the shear stresses
Convention
X
xy
is the stress on the face
perpendicular to the x-axis and points
in the +ve y direction
Total of 9 stress components of which
only 6 are independent since
x x
y y
yx xy
X X
X X
X X
!
!
!
The stress vector is therefore
Strains: 6 independent strain components

|
!
zx
yz
xy
z
y
x
K
K
K
I
I
I
I
Consider the equilibrium of a differential volume element to
obtain the 3 equilibrium equations of elasticity
0
0
0
!
x
x

x
x

x
x
!
x
x

x
x

x
x
!
x
x

x
x

x
x
c
z
yz
xz
b
yz y xy
a
xz
xy
x
X
z y x
X
z y x
X
z y x
o
X
X
X o X
X
X
o
Compactly;
0 = + x X
T
W

x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
! x
x z
y z
x y
z
y
x
0
0
0
0 0
0 0
0 0
where
EQUILIBRIUM
EQUATIONS
(1)
3D elasticity problem is completely defined once we
understand the following three concepts
Strong formulation (governing differential equation +
boundary conditions)
Strain-displacement relationship
Stress-strain relationship
1. Strong formulation of the 3D elasticity problem: Given the
externally applied loads (on S
T
and in V) and the specified
displacements (on S
u
) we want to solve for the resultant
displacements, strains and stresses required to maintain
equilibrium of the body.
x
y
z
S
u
S
T
Volume (V)
u
v
w
x
X
a
dV
X
b
dV
X
c
dV
Volume
element dV
p
y
p
z
p
x
V in X
T
0 = + x W Equilibrium equations
(1)
Boundary conditions
1. Displacement boundary conditions: Displacements are specified on
portion S
u
of the boundary
u
specified
S on u u =
2. Traction (force) boundary conditions: Tractions are specified on
portion S
T
of the boundary
Now, how do I express this mathematically?
x
y
z
S
u
S
T
Volume (V)
u
v
w
x
X
a
dV
X dV
X
c
dV
Volume
element dV
p
y
p
z
p
x
Traction: Distri uted
force per unit area

!
z
y
x
p
p
p
T
S
Traction: Distributed
force per unit area

|
!
z
y
x
p
p
p
T
S
n
n
x
n
y
n
z
S
T
T
S
p
y
p
x
p
z
If the unit outward normal to S
T
:

|
!
z
y
x
n
n
n
n
Then
z z y zy x xz
z yz y y x xy
z xz y xy x x
n n n
n n n
n n n
o X X
X o X
X X o
!
!
!
z
y
x
p
p
p
n
x
n
y
S
T
In 2D
dy
dx
ds
x
y
n
U
U
x
y
n
ds
dy
n
ds
dx
! !
! !
U
U
cos
sin
T
S
p
y
p
x
U
dy
dx
ds
W
x
W
y
X
xy
X
xy
Consider the equilibrium of the wedge in
x-direction
y xy x x x
xy x x
xy x x
n n p
ds
dx
ds
dy
p
dx dy ds p
X W
X W
X W
+ =
+ =
+ =
Similarly
y y x xy y
n n p W X + =
3D elasticity problem is completely defined once we
understand the following three concepts
Strong formulation (governing differential equation +
boundary conditions)
Strain-displacement relationship
Stress-strain relationship
2. Strain-displacement relationships:
x
w
z
u
y
w
z
v
x
v
y
u
z
w
y
v
x
u
zx
yz
xy
z
y
x
x
x

x
x
!
x
x

x
x
!
x
x

x
x
!
x
x
!
x
x
!
x
x
!
K
K
K
I
I
I
Compactly; u x = I

x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
= x
x z
y z
x y
z
y
x
0
0
0
0 0
0 0
0 0

|
!
w
v
u
u

|
!
zx
yz
xy
z
y
x
K
K
K
I
I
I
I
(2)
x
y
A
B
C
A
B
C
v
u
dy
dx
dx
x
v
x
x
x d
x
u
u
x
x

dy
y
u
x
x
dy
y
v
v
x
x

x
u
x
v
tan tan ) B' A' (C' angle
2

y
v
dy
dy v dy
y
v
v dy
AC
AC C' A'
x
u
dx
dx u dx
x
u
u dx
AB
AB B' A'
2 1 2 1
x
x

x
x
}
} = =
x
x
=

'
+

'

'
+

'

x
x

=

=
x
x
=

'
+

'

'
+

'

x
x

=

=
xy
y
x
K
I
I
1
F
2
F
In 2D
3D elasticity problem is completely defined once we
understand the following three concepts
Strong formulation (governing differential equation +
boundary conditions)
Strain-displacement relationship
Stress-strain relationship
3. Stress-Strain relationship:
Linear elastic material (Hookes Law)
I W D = (3)
Linear elastic isotropic material

+
=
2
2 1
0 0 0 0 0
0
2
2 1
0 0 0 0
0 0
2
2 1
0 0 0
0 0 0 1
0 0 0 1
0 0 0 1
) 2 1 )( 1 (
+
+
+
+ + +
+ + +
+ + +
+ +
E
D
Special cases:
1. 1D elastic bar (only 1 component of the stress (stress) is
nonzero. All other stress (strain) components are zero)
Recall the (1) equilibrium, (2) strain-displacement and (3) stress-
strain laws
2. 2D elastic problems: 2 situations
PLANE STRESS
PLANE STRAIN
3. 3D elastic problem: special case-axisymmetric body with
axisymmetric loading (we will skip this)
PLANE STRESS: Only the in-plane stress components are nonzero
x
y
Area
element dA
Nonzero stress components
xy y x
X W W , ,
y
W
x
W
xy
X
xy
X
h
D
Assumptions:
1. h<<D
2. Top and bottom surfaces are free from
traction
3. X
c
=0 and p
z
=0
PLANE STRESS Examples:
1. Thin plate with a hole
2. Thin cantilever plate
y
o
x
o
xy
X
xy
X
Nonzero strains:
xy z y x
K I I I , , ,
Isotropic linear elastic stress-strain law

xy
y
x
xy
y
x
E
K
I
I
+
+
+
+
X
W
W
2
1
0 0
0 1
0 1
1
2
Hence, the D matrix for the plane stress case is

=
2
1
0 0
0 1
0 1
1
2
+
+
+
+
E
D
I W D =
)
y x z
I I
+
+
I +

=
1
Nonzero stresses:
xy y x
X o o , ,
PLANE STRESS
PLANE STRAIN: Only the in-plane strain components are nonzero
Area
element dA
Nonzero strain components
y
I
I
y
K
y
K
Assumptions:
1. Displacement components u,v functions
of (x,y) only and w=0
2. Top and bottom surfaces are fixed
3. X
c
=0
4. p
x
and p
y
do not vary with z
xy y x
K I I , ,
x
y
z
PLANE STRAIN Examples:
1. Dam
2. Long cylindrical pressure vessel subjected to internal/external
pressure and constrained at the ends
1
Slice of unit
thickness
x
y
z
y
W
x
W
xy
X
xy
X
z
W
Nonzero stress:
Isotropic linear elastic stress-strain law
) )

)

+
=

xy
y
x
xy
y
x
E
K
I
I
+
+ +
+ +
+ +
X
W
W
2
2 1
0 0
0 1
0 1
2 1 1
Hence, the D matrix for the plane strain case is
) )

+
=
2
2 1
0 0
0 1
0 1
2 1 1
+
+ +
+ +
+ +
E
D
I W D =
)
z x y
W + W W = +
xy z y x
X W W W , , ,
Nonzero strain components:
xy y x
K I I , ,
PLANE STRAIN
Example problem
x
y
3
2
1
4
2
2
The square block is in plane strain
and is subjected to the following
strains
3 2
2
3
2
y x
xy
xy
xy
y
x
=
=
=
K
I
I
Compute the displacement field (i.e., displacement components
u(x,y) and v(x,y)) within the block
Solution
Recall from definition
) 3 (
) 2 ( 3
) 1 ( 2
3 2
2
y x
x
v
y
u
xy
y
v
xy
x
u
xy
y
x
+ =
x
x
+
x
x
=
=
x
x
=
=
x
x
=
K
I
I
Integrating (1) and (2)
) 5 ( ) ( ) , (
) 4 ( ) ( ) , (
2
3
1
2
x C xy y x v
y C y x y x u
+ =
+ =
Arbitrary function of x
Arbitrary function of y
Plug expressions in (4) and (5) into equation (3)
? A ? A
0
) ( ) (
) ( ) (
) ( ) (
) 3 (
2 1
3 2
2
3
1
2
3 2
2
3
1
2
3 2
=
x
x
+
x
x

+ =
x
x
+ +
x
x
+
+ =
x
+ x
+
x
+ x

+ =
x
x
+
x
x
x
x C
y
y C
y x
x
x C
y
y
y C
x
y x
x
x C xy
y
y C y x
y x
x
v
y
u
Function of y
Function of x
) constant a (
) ( ) (
2 1
C
x
x C
y
y C
=
x
x
=
x
x
Hence
Integrate to obtain
2 2
1 1
) (
) (
D Cx x C
D Cy y C
+
+ =
D
1
and D
2
are two constants of
integration
Plug these back into equations (4) and (5)
2
3
1
2
) , ( ) 5 (
) , ( ) 4 (
D Cx xy y x v
D Cy y x y x u
!
!
How to find C, D
1
and D
2
?
Use the 3 boundary conditions
0 ) 0 , 2 (
0 ) 0 , 0 (
0 ) 0 , 0 (
=
=
=
v
v
u
To obtain
0
0
0
2
1
!
!
!
D
D
C
Hence the solution is
3
2
) , (
) , (
xy y x v
y x y x u
=
=
x
y
3
2
1
4
2
2
Principle of Minimum Potential Energy
Definition: For a linear elastic body subjected to body forces
X=[X
a
,X
b
,X
c
]
T
and surface tractions T
S
=[p
x
,p
y
,p
z
]
T
, causing
displacements u=[u,v,w]
T
and strains I and stresses W, the potential
energy 4 is defined as the strain energy minus the potential energy
of the loads involving X and T
S
4=U-W
x
y
z
S
u
S
T
Volume (V)
u
v
x
X
a
dV
X
b
dV
X
c
dV
Volume
element dV
p
y
p
z
p
x

!
!
T
S
S
T
V
T
V
T
dS T u dV X u
dV
W
2
1
U I W
Strain energy of the elastic body

= =
V
T
V
T
dV D dV I I I W
2
1
2
1
U
I W D =
Using the stress-strain law
In 1D

!
! ! !
L
x V V
Adx E dV E dV
0
2 2
2
1
2
1
2
1
U I I oI
In 2D plane stress and plane strain
)

!
V
xy xy y y x x
dV K X I o I o
2
1
U
Why?
Principle of minimum potential energy: Among all admissible
displacement fields the one that satisfies the equilibrium equations
also render the potential energy 4 a minimum.
admissible displacement field:
1. first derivative of the displacement components exist
2. satisfies the boundary conditions on S
u